二分图

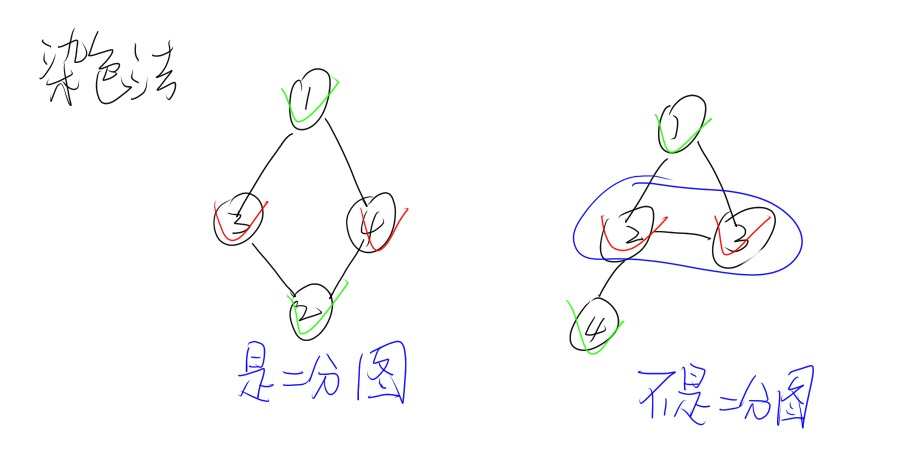
二分图:当一个图的顶点可以被分为两个集合,且任意一条边的两个端点属于不同集合时为二分图
即:相邻两个点位于不同集合内
一个图是二分图当且仅当图中不含有奇数环(长度为奇数的环)
染色法
可以把二分图看作染色
用途:判断二分图

做法:循环,若一个点未被染色,用$DFS$染色,若冲突,则不是二分图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| #include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,M=1e5+5;
int h[N],ne[2*M],to[2*M];
int cnt;
void addedge(int u,int v){
ne[++cnt]=h[u];
to[cnt]=v;
h[u]=cnt;
}
int n,m;
int color[N];
bool dfs(int now,int col){
color[now]=col;
for(int i=h[now];i;i=ne[i]){
if(!color[to[i]]){
if(!dfs(to[i],3-col))return 0;
}
if(color[to[i]]==color[now])return 0;
}
return 1;
}
int main(){
cin >> n >> m;
for(int i=1;i<=m;i++){
int u,v;
cin >> u >> v;
addedge(u,v);
addedge(v,u);
}
bool flag=1;
for(int i=1;i<=n;i++){
if(!color[i]){
if(!dfs(i,1)){
flag=0;
break;
}
}
}
if(flag){
cout << "Yes";
}
else{
cout << "No";
}
return 0;
}
|
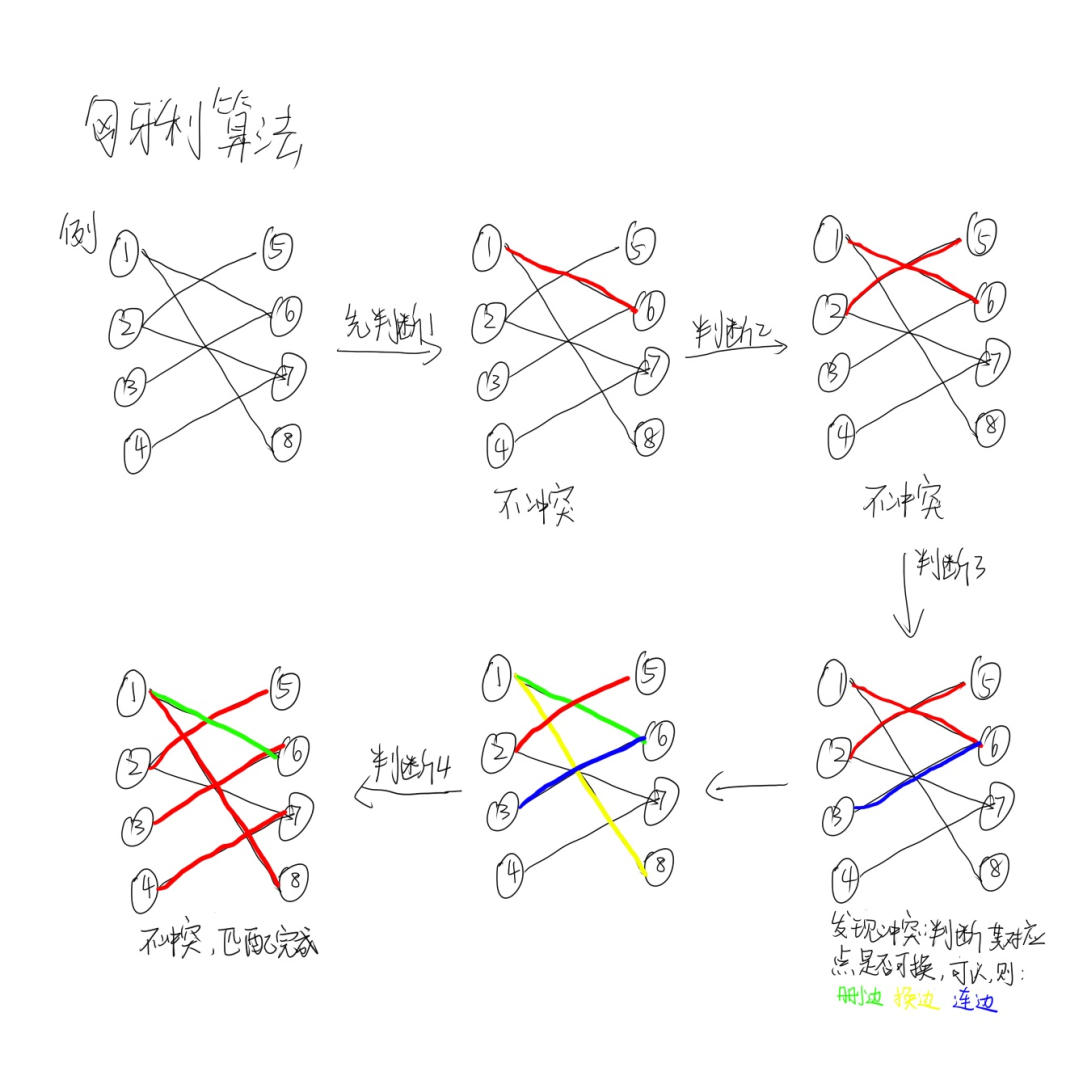
匈牙利算法
作用:求二分图的最大匹配
二分图的匹配:给定一个二分图 $G$,在 $G$ 的一个子图 $M$ 中,$M$ 的边集 ${E}$ 中的任意两条边都不依附于同一个顶点,则称 $M$ 是一个匹配。
二分图的最大匹配:所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配,其边数即为最大匹配数。
思路:
循环左侧的每一个点,从头匹配,若当前边的终点未被考虑过,若这个点未被匹配或已经被匹配的对应点可以匹配另外一个,则当前点匹配终点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| #include<bits/stdc++.h>
using namespace std;
const int N=505,M=1e5+5;
int nl[N],nr[N];
int h[N],ne[M],to[M];
int cnt;
void addedge(int u,int v){
ne[++cnt]=h[u];
to[cnt]=v;
h[u]=cnt;
}
int n1,n2,m;
bool st[N];
int match[N];
bool find(int x){
for(int i=h[x];i;i=ne[i]){
if(!st[to[i]]){
st[to[i]]=1;
if(match[to[i]]==0||find(match[to[i]])){
match[to[i]]=x;
return 1;
}
}
}
return 0;
}
int main(){
cin >> n1 >> n2 >> m;
for(int i=1;i<=m;i++){
int u,v;
cin >> u >> v;
addedge(u,v);
}
int ans=0;
for(int i=1;i<=n1;i++){
memset(st,0,sizeof st);
if(find(i))ans++;
}
cout << ans;
return 0;
}
|