基础优化技巧

三分

三分用来解决求单峰函数的极值点的问题。

单峰函数：在所考虑的区间中只有一个极值点的函数。

例题：[洛谷P3382 三分](P3382 三分)

三分

题目背景

本题可能存在严重精度问题，部分数据下难以通过。本题数据较水，仅供参考。

题目描述

如题，给出一个 $N$ 次函数，保证在范围 $[l, r]$ 内存在一点 $x$，使得 $[l, x]$ 上单调增，$[x, r]$ 上单调减。试求出 $x$ 的值。

输入格式

第一行一次包含一个正整数 $N$ 和两个实数 $l, r$，含义如题目描述所示。

第二行包含 $N + 1$ 个实数，从高到低依次表示该 $N$ 次函数各项的系数。

输出格式

输出为一行，包含一个实数，即为 $x$ 的值。若你的答案满足以下二者之一，则算正确：

• 你的答案 $x’$ 与标准答案 $x$ 的相对或绝对误差不超过 $10^{-5}$。
• 你的答案 $x’$ 与标准答案 $x$ 对应的函数值，即 $f(x’) $ 和 $f(x)$ 的相对或绝对误差不超过 $10^{-5}$。

样例 #1

样例输入 #1

1 2	3 -0.9981 0.5 1 -3 -3 1

样例输出 #1

1

-0.41421

提示

对于 $100%$ 的数据，$6 \le N \le 13$，函数系数均在 $[-100,100]$ 内且至多 $15$ 位小数，$|l|,|r|\leq 10$ 且至多 $15$ 位小数。$l\leq r$。

【样例解释】

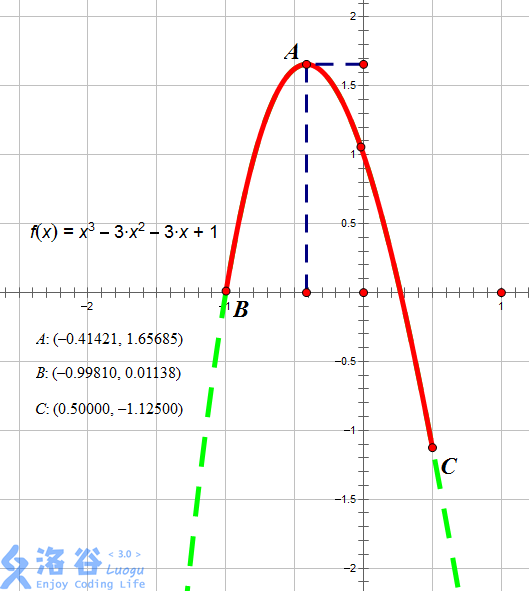
如图所示，红色段即为该函数 $f(x) = x^3 - 3 x^2 - 3x + 1$ 在区间 $[-0.9981, 0.5]$ 上的图像。

当 $x = -0.41421$ 时图像位于最高点，故此时函数在 $[l, x]$ 上单调增，$[x, r]$ 上单调减，故 $x = -0.41421$，输出 $-0.41421$。

分析：

令 $lmid, rmid$ 是区间任意的两个分段点，把区间分成三段。丢弃极值点一定不在的那一段区间， 使得区间长度缩小。

以这题上凸的函数为例子， 当$ f (lmid) > f (rmid)$ 的时候， 丢弃 $(rmid, R)$ 这一段， 令 $R = rmid$ 继续循环， 反之则丢弃$ (L, lmid) $这 一段。

上凸函数 : 开口向下的单峰函数

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

#include<bits/stdc++.h>
using namespace std;

const int N=15;

int n;
double l,r;
double num[N];

double f(double x){
    double ans=0,tmp=1;
    for(int i=1;i<=n+1;i++,tmp*=x){
        ans+=tmp*num[i];
    }
    return ans;
}

int main(){
    
    cin >> n >> l >> r;
    for(int i=n+1;i>=1;i--){
        cin >> num[i];
    }
    while(r-l>1e-10){
        double len=(r-l)/3.0;
        double lmid=l+len,rmid=r-len;
        if(f(lmid)<f(rmid))l=lmid;
        else r=rmid;
    }
    cout << fixed << setprecision(10) << l;
    return 0;
}

可以发现其实只会丢掉最两边的段， 中间这一段不会丢， 可以让两边的段尽量长。

那么我们令 $lmid = mid – delta, rmid = mid + delta$, 这样每次可以让区间长度缩小一半, 其中 $delta$ 是一个很小的量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

#include<bits/stdc++.h>
using namespace std;

const int N=15;

int n;
double l,r;
double num[N];

double f(double x){
    double ans=0,tmp=1;
    for(int i=1;i<=n+1;i++,tmp*=x){
        ans+=tmp*num[i];
    }
    return ans;
}

int main(){
    
    cin >> n >> l >> r;
    for(int i=n+1;i>=1;i--){
        cin >> num[i];
    }
    while(r-l>1e-10){
        double delta=(r-l)/10000.0,mid=(l+r)/2.0;
        double lmid=mid-delta,rmid=mid+delta;
        if(f(lmid)<f(rmid))l=lmid;
        else r=rmid;
    }
    cout << fixed << setprecision(10) << l;
    return 0;
}

当然也是可以二分斜率的。

二分斜率的时候为了避免求导， 可以计算 $f(mid), f (mid + delta)$ 的值， 其中 $delta$ 是一个很小的数来判断怎么取舍区间。

代码与上面相同。

01分数规划

形如： 有 $n$ 个物品， 每个物品有两个权值 $a, b$ ， 然后让你选出一些物品使得两个权值和的比值最大或者最小。 也就是令 $w_i$ 表示选 ($w_i = 1$) 或者不选 ($w_i = 0$)，最大或者最小化下列值:
$$
\frac{\sum w_i\times a_i}{\sum w_i \times b_i}
$$
除此之外，一般还会对选择的件数或者是选择的物品给出一些限制。

一般来说我们使用二分求解。二分一个值$t$以后，得到：
$$
\frac{\sum w_i\times a_i}{\sum w_i \times b_i} \ge t
$$
意思是二分一个值，然后判定能不能大于这个值，然后移项：
$$
\sum w_i \times(a_i-t\times b_i)\ge 0
$$

例题：洛谷P3199 [HNOI2009] 最小圈

[HNOI2009] 最小圈

题目描述

考虑带权有向图 $G=(V,E)$ 以及 $w:E\rightarrow \R$，每条边 $e=(i,j)$（$i\neq j$，$i, j\in V$）的权值定义为 $w_{i,j}$。设 $n=|V|$。

$c=(c_1,c_2,\cdots,c_k)$（$c_i\in V$）是 $G$ 中的一个圈当且仅当 $(c_i,c_{i+1})$（$1\le i<k$）和 $(c_k,c_1)$ 都在 $E$ 中。称 $k$ 为圈 $c$ 的长度，同时记 $c_{k+1}=c_1$，并定义圈 $c=(c_1,c_2,\cdots,c_k)$ 的平均值为
$$
\mu(c)= \frac 1 k \sum\limits_{i=1}^{k} w_{c_i,c_{i+1}}
$$
即 $c$ 上所有边的权值的平均值。设 $\mu’(G)=\min_c\mu(c)$ 为 $G$ 中所有圈 $c$ 的平均值的最小值。

给定图 $G=(V,E)$ 以及 $w:E\rightarrow \R$，求出 $G$ 中所有圈 $c$ 的平均值的最小值 $\mu’(G)$。

输入格式

第一行两个正整数，分别为 $n$ 和 $m$，并用一个空格隔开。其中 $n=|V|$，$m=|E|$ 分别表示图中有 $n$ 个点 和 $m$ 条边。

接下来 $m$ 行，每行三个数 $i,j,w_{i,j}$，表示有一条边 $(i,j)$ 且该边的权值为 $w_{i,j}$，注意边权可以是实数。输入数据保证图 $G=(V,E)$ 连通，存在圈且有一个点能到达其他所有点。

输出格式

一个实数 $\mu’(G)$，要求精确到小数点后 $8$ 位。

样例 #1

样例输入 #1

1 2 3 4 5 6

4 5 1 2 5 2 3 5 3 1 5 2 4 3 4 1 3

样例输出 #1

1	3.66666667

样例 #2

样例输入 #2

1 2 3

2 2 1 2 -2.9 2 1 -3.1

样例输出 #2

1	-3.00000000

提示

对于 $100%$ 的数据，$2\leq n\le 3000$，$1\leq m\le 10000$，$|w_{i,j}| \le 10^7$，$1\leq i, j\leq n$ 且 $i\neq j$。

形式化题面：

给一张 $n$ 个点 $m$ 条边的有向带权图，在图中找一个环，使得环上边权之和除以节点个数最小，求这个最小平均值。

分析：

设第$i$条边的边权为$w_i$，环上有$k$个点，每个环上的边数与点数一定相等，则要求的就是$\frac{\sum_{i=1}^{k} w_i}{k}$的最小值。

观察到答案是一个“比率” 的形式，联想到分数规划问题。 二分一个答案 $t$ 后，需要判断：
$$
\frac{\sum_{i=1}^{k} w_i}{k}\le t
$$
若满足，则继续二分$[l,t]$即可，下面考虑如何判断。

不等式移项得：
$$
\sum_{i=1}^{k} w_i-k\times t=\sum_{i=1}^{k}(w_i-t) <0
$$
因此，只需要把第$i$条边的边权改成$w_i-t$，SPFA判断负环即可，时间复杂度$O(\log_2v\times n\times m)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

#include<bits/stdc++.h>
using namespace std;

const int N=3005,M=1e4+5;
int n,m;
int h[N],ne[M],to[M];
double e[M];
int idx;
void addedge(int u,int v,double w){
    ne[++idx]=h[u];
    h[u]=idx;
    to[idx]=v;
    e[idx]=w;
}

double d[N];
int cnt;
bool vis[N];
bool spfa(double t){
    queue<int>q;
    for(int i=1;i<=n;i++){
        d[i]=0;
        q.push(i);
        vis[i]=true;
    }
    cnt=0;
    while(!q.empty()){
        int u=q.front();
        q.pop();
        vis[u]=false;
        
        for(int i=h[u];i;i=ne[i]){
            if(d[to[i]]-(d[u]+e[i]-t)>1e-10){
                d[to[i]]=d[u]+e[i]-t;
                
                cnt++;
                if(cnt>11*n)return true;
                if(!vis[to[i]]){
                    vis[to[i]]=true;
                    q.push(to[i]);
                }
            }
        }
    }
    
    return 0;
}

int main(){
    cin >> n >> m;
    for(int i=1;i<=m;i++){
        int u,v;
        double w;
        cin >> u >> v >> w;
        addedge(u,v,w);
    }
    double l=-1e7,r=1e7;
    while(r-l>1e-10){
        double mid=(l+r)/2.0;
        if(spfa(mid))r=mid-1e-10;
        else l=mid+1e-10;
    }
    cout << fixed << setprecision(8) << l;
    return 0;
}

整体二分

有多个需要二分的对象的时候，有时候可以放在一起来二分。

例题：洛谷P3527 [POI2011] MET-Meteors

[POI2011] MET-Meteors

题面翻译

Byteotian Interstellar Union

有 $n$ 个成员国。现在它发现了一颗新的星球，这颗星球的轨道被分为 $m$ 份（第 $m$ 份和第 $1$ 份相邻），第 $i$ 份上有第 $a_i$ 个国家的太空站。

这个星球经常会下陨石雨。BIU 已经预测了接下来 $k$ 场陨石雨的情况。

BIU 的第 $i$ 个成员国希望能够收集 $p_i$ 单位的陨石样本。你的任务是判断对于每个国家，它需要在第几次陨石雨之后，才能收集足够的陨石。

输入格式

第一行是两个数 $n,m$。

第二行有 $m$ 个数，第 $i$ 个数 $o_i$ 表示第 $i$ 段轨道上有第 $o_i$ 个国家的太空站。

第三行有 $n$ 个数，第 $i$ 个数 $p_i$ 表示第 $i$ 个国家希望收集的陨石数量。

第四行有一个数 $k$，表示 BIU 预测了接下来的 $k$ 场陨石雨。 接下来 $k$ 行，每行有三个数 $l_i,r_i,a_i$ ，表示第 $k$ 场陨石雨的发生地点在从 $l_i$ 顺时针到 $r_i$ 的区间中（如果 $l_i \leq r_i$，则是 $l_i, l_i + 1
\cdots, r_i$，否则就是 $l_i, l_i + 1,
\cdots m - 1, m, 1, 2, \cdots r_i$），向区间中的每个太空站提供 $a_i$ 单位的陨石样本。

输出格式

输出 $n$ 行。第 $i$ 行的数 $w_i$ 表示第 $i$ 个国家在第 $w_i$ 波陨石雨之后能够收集到足够的陨石样本。如果到第 $k$ 波结束后仍然收集不到，输出 NIE。

数据范围

$1\le n,m,k\le 3\cdot10^5$；

$1\le p_i,a_i\le 10^9$；

题目描述

Byteotian Interstellar Union (BIU) has recently discovered a new planet in a nearby galaxy. The planet is unsuitable for colonisation due to strange meteor showers, which on the other hand make it an exceptionally interesting object of study.

The member states of BIU have already placed space stations close to the planet’s orbit. The stations’ goal is to take samples of the rocks flying by.

The BIU Commission has partitioned the orbit into $m$ sectors, numbered from $1$ to $m$, where the sectors $1$ and $m$ are adjacent. In each sector there is a single space station, belonging to one of the $n$ member states.

Each state has declared a number of meteor samples it intends to gather before the mission ends. Your task is to determine, for each state, when it can stop taking samples, based on the meter shower predictions for the years to come.

输入格式

The first line of the standard input gives two integers, $n$ and $m$ ($1\le n,m\le 300\ 000$), separated by a single space, that denote,respectively, the number of BIU member states and the number of sectors the orbit has been partitioned into.

In the second line there are $m$ integers $o_i$ ($1\le o_i\le n$),separated by single spaces, that denote the states owning stations in successive sectors.

In the third line there are $n$ integers $p_i$ ($1\le p_i\le 10^9$),separated by single spaces, that denote the numbers of meteor samples that the successive states intend to gather.

In the fourth line there is a single integer $k$ ($1\le k\le 300\ 000$) that denotes the number of meteor showers predictions. The following $k$ lines specify the (predicted) meteor showers chronologically. The $i$-th of these lines holds three integers $l_i,r_i,a_i$ (separated by single spaces), which denote that a meteor shower is expected in sectors $l_i,l_{i+1},…,r_i$(if $l_i\le r_i$) or sectors $l_i,l_{i+1},…,m,1,…,r_i$ (if $l_i>r_i$) , which should provide each station in those sectors with $a_i$ meteor samples ($1\le a_i\le 10^9$).

输出格式

Your program should print $n$ lines on the standard output.

The $i$-th of them should contain a single integer $w_i$, denoting the number of shower after which the stations belonging to the $i$-th state are expected to gather at least $p_i$ samples, or the word NIE (Polish for no) if that state is not expected to gather enough samples in the foreseeable future.

样例 #1

样例输入 #1

1 2 3 4 5 6 7

3 5 1 3 2 1 3 10 5 7 3 4 2 4 1 3 1 3 5 2

样例输出 #1

1 2 3

3 NIE 1

考虑对所有国家同时进行二分， 使用数组存当前要处理的所有国家， 定义一个函数 $solve (v, L, R)$ 表示当前要处理 $v$ 中的国家， 可能的答案区间是 $[L, R]$，二分出一个 $mid = (L + R) / 2$ 以后，递归处理 $solve (vl, L, mid)$ 和 $solve (vr, mid + 1, R)$。 其中 $vl$ 是答案小于等于 $mid$ 的国家， $vr$ 是答案大于 $mid$ 的国家。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103

#include<bits/stdc++.h>
using namespace std;

const int N=3e5+5;
typedef long long ll;
ll n,m;
ll ans[N];
ll k;
struct que{
    ll l,r,a,id;
}e[N];
ll tr[2*N];
struct node{
    ll need,id;
}p[N],p1[N],p2[N];
vector<ll>q[N];
ll lowbit(ll x){
    return x&-x;
}

void add(ll x,ll k){
    for(ll i=x;i<=2*m;i+=lowbit(i)){
        tr[i]+=k;
    }
}

ll query(ll x){
    ll res=0;
    for(ll i=x;i;i-=lowbit(i)){
        res+=tr[i];
    }
    return res;
}

ll get(ll x){
    ll res=0;
    for(ll i=0;i<q[p[x].id].size();i++){
        res+=query(q[p[x].id][i])+query(q[p[x].id][i]+m);
        if(res>=p[x].need)return res;
    }
    return res;
}

void merge(ll l,ll r,ll L,ll R){
    if(L>R)return;
    if(l==r){
        for(ll i=L;i<=R;i++){
            ans[p[i].id]=l;
        }
        return;
    }
    ll mid=l+r>>1;
    ll cnt1=0,cnt2=0;
    for(ll i=l;i<=mid;i++){
        add(e[i].l,e[i].a);add(e[i].r+1,-e[i].a);
    }
    for(ll i=L;i<=R;i++){
        ll tmp=get(i);
        if(tmp>=p[i].need)p1[++cnt1]=p[i];
        else p[i].need-=tmp,p2[++cnt2]=p[i];
    }
    
    for(ll i=l;i<=mid;i++){
        add(e[i].l,-e[i].a);add(e[i].r+1,e[i].a);
    }
    
    for(ll i=L;i<=L+cnt1-1;i++){
        p[i]=p1[i-L+1];
    }
    for(ll i=L+cnt1;i<=R;i++){
        p[i]=p2[i-L-cnt1+1];
    }
    
    merge(l,mid,L,L+cnt1-1);
    merge(mid+1,r,L+cnt1,R);
}

int main(){
    cin >> n >> m;
    for(ll i=1;i<=m;i++){
        ll x;
        cin >> x;
        q[x].push_back(i);
    }
    for(ll i=1;i<=n;i++){
        cin >> p[i].need;
        p[i].id=i;
    }
    cin >> k;
    for(ll i=1;i<=k;i++){
        cin >> e[i].l >> e[i].r >> e[i].a;
        e[i].id=i;
        if(e[i].r<e[i].l)e[i].r+=m;
    }
    k++;
    e[k].l=1,e[k].r=2*m,e[k].a=1000000000;
    merge(1,k,1,n);
    for(ll i=1;i<=n;i++){
        if(ans[i]==k)cout << "NIE\n";
        else cout << ans[i] << '\n';
    }
    return 0;
}

分治

主要思想是把大问题分成小问题再合并起来。

所以一般要求问题有可分性，同时有可合并性。

例题1：洛谷P3810 【模板】三维偏序（陌上花开）

【模板】三维偏序（陌上花开）

题目背景

这是一道模板题，可以使用 bitset，CDQ 分治，KD-Tree 等方式解决。

题目描述

有 $ n $ 个元素，第 $ i $ 个元素有 $ a_i,b_i,c_i $ 三个属性，设 $ f(i) $ 表示满足 $ a_j \leq a_i $ 且 $ b_j \leq b_i $ 且 $ c_j \leq c_i $ 且 $ j \ne i $ 的 $j$ 的数量。

对于 $ d \in [0, n) $，求 $ f(i) = d $ 的数量。

输入格式

第一行两个整数 $ n,k $，表示元素数量和最大属性值。

接下来 $ n $ 行，每行三个整数 $ a_i ,b_i,c_i $，分别表示三个属性值。

输出格式

$ n $ 行，第 $ d + 1 $ 行表示 $ f(i) = d $ 的 $ i $ 的数量。

样例 #1

样例输入 #1

1 2 3 4 5 6 7 8 9 10 11

10 3 3 3 3 2 3 3 2 3 1 3 1 1 3 1 2 1 3 1 1 1 2 1 2 2 1 3 2 1 2 1

样例输出 #1

1 2 3 4 5 6 7 8 9 10

3 1 3 0 1 0 1 0 0 1

提示

$ 1 \leq n \leq 10^5$，$1 \leq a_i, b_i, c_i \le k \leq 2 \times 10^5 $。

分析：

排序解决一个维度，分治解决一个维度，剩下的维度使用树状数组解决。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+5,M=2e5+5;

int n,m;
struct Data{
    int a,b,c,res,s;
    bool operator<(const Data& t)const{
        if(a!=t.a)return a<t.a;
        if(b!=t.b)return b<t.b;
        return c<t.c;
    }
    bool operator==(const Data& t)const{
        return a==t.a&&b==t.b&&c==t.c;
    }
}q[N],w[N];
int tr[M],ans[N];

int lowbit(int x){
    return x&-x;
}

void add(int x,int v){
    for(int i=x;i<M;i+=lowbit(i)){
        tr[i]+=v;
    }
}

int query(int x){
    int res=0;
    for(int i=x;i;i-=lowbit(i)){
        res+=tr[i];
    }
    return res;
}

void merge_sort(int l,int r){
    if(l>=r)return;
    int mid=l+r>>1;
    merge_sort(l,mid),merge_sort(mid+1,r);
    int i=l,j=mid+1,k=0;
    while(i<=mid&&j<=r){
        if(q[i].b<=q[j].b){
            add(q[i].c,q[i].s),w[k++]=q[i++];
        }
        else{
            q[j].res+=query(q[j].c),w[k++]=q[j++];
        } 
    }
    while(i<=mid){
        add(q[i].c,q[i].s),w[k++]=q[i++];
    }
    while(j<=r){
        q[j].res+=query(q[j].c),w[k++]=q[j++];
    }
    for(int i=l;i<=mid;i++){
        add(q[i].c,-q[i].s);
    }
    for(int i=l,j=0;j<k;i++,j++){
        q[i]=w[j];
    }
}
int main(){
    cin >> n >> m;
    for(int i=0;i<n;i++){
        cin >> q[i].a >> q[i].b >> q[i].c;
        q[i].s=1;
    }
    sort(q,q+n);
    
    int k=1;
    for(int i=1;i<n;i++){
        if(q[i]==q[k-1])q[k-1].s++;
        else q[k++]=q[i];
    }
    merge_sort(0,k-1);
    for(int i=0;i<k;i++){
        ans[q[i].res+q[i].s-1]+=q[i].s;
    }
    for(int i=0;i<n;i++){
        cout << ans[i] << endl;
    }
    return 0;
}

例题2：洛谷P3350 [ZJOI2016] 旅行者

[ZJOI2016] 旅行者

题目描述

小 Y 来到了一个新的城市旅行。她发现了这个城市的布局是网格状的，也就是有 $n$ 条从东到西的道路和 $m$ 条从南到北的道路，这些道路两两相交形成 $n\times m$ 个路口 $(i,j)$， $(1\leq i\leq n,1\leq j\leq m)$

她发现不同的道路路况不同，所以通过不同的路口需要不同的时间。通过调查发现，从路口 $(i,j)$ 到路口 $(i,j+1)$ 需要时间 $r(i,j)$ ，从路口 $(i,j)$ 到路口 $(i+1,j)$ 需要时间 $c(i,j)$ 。注意这里的道路是双向的。小 Y 有 $q$ 个询问，她想知道从路口 $(x1,y1)$ 到路口 $(x2,y2)$ 最少需要花多少时间。

输入格式

第一行包含 2 个正整数 $n,m$ 表示城市的大小。

接下来 $n$ 行，每行包含 $m-1$ 个整数，第 $i$ 行第 $j$ 个正整数表示从一个路口到另一个路口的时间 $r(i,j)$ 。

接下来 $n-1$ 行，每行包含 $m$ 个整数，第 $i$ 行第 $j$ 个正整数表示从一个路口到另一个路口的时间 $c(i,j)$。

接下来一行，包含一个正整数 $q$，表示小 Y 的询问个数。

接下来 $q$ 行，每行包含 $4$ 个正整数 $x1,y1,x2,y2$，表示两个路口的位置。

输出格式

输出共 $q$ 行，每行包含一个整数表示从一个路口到另一个路口最少需要花的时间。

样例 #1

样例输入 #1

1 2 3 4 5 6 7

2 2 2 3 6 4 2 1 1 2 2 1 2 2 1

样例输出 #1

1 2

6 7

提示

数据规模与约定

• $n\times m \le 2\times 10^4$。
• $q \le 10^5$。
• $1 \le r(i,j),c(i,j) \le 10^4$。

例题3：洛谷CF1156E Special Segments of Permutation

Special Segments of Permutation

题面翻译

给定一个长度为 $n$ 的排列 $p$，求有多少区间 $[l,r]$ 满足，$p_l+p_r=\max\limits_{i=l}^r{p_i}$。

题目描述

You are given a permutation $ p $ of $ n $ integers $ 1 $ , $ 2 $ , …, $ n $ (a permutation is an array where each element from $ 1 $ to $ n $ occurs exactly once).

Let’s call some subsegment $ p[l, r] $ of this permutation special if $ p_l + p_r = \max \limits_{i = l}^{r} p_i $ . Please calculate the number of special subsegments.

输入格式

The first line contains one integer $ n $ ( $ 3 \le n \le 2 \cdot 10^5 $ ).

The second line contains $ n $ integers $ p_1 $ , $ p_2 $ , …, $ p_n $ ( $ 1 \le p_i \le n $ ). All these integers are pairwise distinct.

输出格式

Print the number of special subsegments of the given permutation.

样例 #1

样例输入 #1

1 2	5 3 4 1 5 2

样例输出 #1

1

2

样例 #2

样例输入 #2

1 2

3 1 3 2

样例输出 #2

1

1

提示

Special subsegments in the first example are $ [1, 5] $ and $ [1, 3] $ .

The only special subsegment in the second example is $ [1, 3] $ .

倍增

一般是处理一个 $f[i][j]$ 表示 $[i, i + 2^k – 1]$ 这个区间或者从某个点开始跳 $2^k$ 步的信息， 然后通过合并两个小区间的信息得到大区间的信息。

LCA, ST 表都是倍增的经典应用。

例题1：洛谷P4155 [SCOI2015] 国旗计划

[SCOI2015] 国旗计划

题目描述

A 国正在开展一项伟大的计划 —— 国旗计划。这项计划的内容是边防战士手举国旗环绕边境线奔袭一圈。这项计划需要多名边防战士以接力的形式共同完成，为此，国土安全局已经挑选了 $N$ 名优秀的边防战上作为这项计划的候选人。

A 国幅员辽阔，边境线上设有 $M$ 个边防站，顺时针编号 $1$ 至 $M$。每名边防战士常驻两个边防站，并且善于在这两个边防站之间长途奔袭，我们称这两个边防站之间的路程是这个边防战士的奔袭区间。$N$ 名边防战士都是精心挑选的，身体素质极佳，所以每名边防战士的奔袭区间都不会被其他边防战士的奔袭区间所包含。

现在，国十安全局局长希望知道，至少需要多少名边防战士，才能使得他们的奔袭区间覆盖全部的边境线，从而顺利地完成国旗计划。不仅如此，安全局局长还希望知道更详细的信息：对于每一名边防战士，在他必须参加国旗计划的前提下，至少需要多少名边防战士才能覆盖全部边境线，从而顺利地完成国旗计划。

输入格式

第一行，包含两个正整数 $N,M$，分别表示边防战士数量和边防站数量。

随后 $N$ 行，每行包含两个正整数。其中第 $i$ 行包含的两个正整数 $C_i$、$D_i$ 分别表示 $i$ 号边防战士常驻的两个边防站编号，$C_i$ 号边防站沿顺时针方向至 $D_i$ 号边防站力他的奔袭区间。数据保证整个边境线都是可被覆盖的。

输出格式

输出数据仅 $1$ 行，需要包含 $N$ 个正整数。其中，第 $j$ 个正整数表示 $j$ 号边防战士必须参加的前提下至少需要多少名边防战士才能顺利地完成国旗计划。

样例 #1

样例输入 #1

1 2 3 4 5

4 8 2 5 4 7 6 1 7 3

样例输出 #1

1

3 3 4 3

提示

$N\leqslant 2×10^5,M<10^9,1\leqslant C_i,D_i\leqslant M$。

分析：

因为不存在一个区间完全包含另外一个区间， 那么把所有区间按照左端点排序， 右端点必然单调增加， 我们总是可以找到以一个战士最远可以跳到的那个战士所在的位置。 我们定义跳到最远那个战士为跳一步。 $F[x][0]$ 表示 $x$ 跳一步可以到的地方，倍增即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

#include<bits/stdc++.h>
using namespace std;

const int N=2e5+5;

int n,m;
struct node{
    int l,r,id;
    bool operator<(const node &x)const{
        if(l==x.l)return r<x.r;
        return l<x.l;
    }
}a[2*N];
int to[2*N][30];
int ans[N];

void solve(int k){
    int rmax=a[k].l+m,p=k,tmp=0;
    for(int i=20;i>=0;i--)
    {
        if(to[k][i]!=0&&a[to[k][i]].r<rmax){
            k=to[k][i];
            tmp+=1<<i;
        }
    }
    ans[a[p].id]=tmp+2;
}
int main(){
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        int l,r;
        cin >> l >> r;
        if(r<l)r+=m;
        a[i]={l,r,i};
    }
    sort(a+1,a+n+1);
    for(int i=1;i<=n;i++){
        a[i+n]=a[i];
        a[i+n].l+=m;
        a[i+n].r+=m;
    }
    
    for(int i=1,j=1;i<=2*n;i++){
        while(a[i].r>=a[j].l&&j<=2*n){
            j++;
        }
        to[i][0]=j-1;
    }
    for(int i=1;i<=20;i++){
        for(int j=1;j<=2*n;j++){
            to[j][i]=to[to[j][i-1]][i-1];
        }
    }
    
    for(int i=1;i<=n;i++){
        solve(i);
    }
    
    for(int i=1;i<=n;i++){
        cout << ans[i] << ' ';
    }
    return 0;
}

例题2：洛谷P9361 [ICPC2022 Xi’an R] Contests

[ICPC2022 Xi’an R] Contests

题面翻译

题目描述

$n$ 个选手参加了 $m$ 场比赛。给出每场比赛的排行榜。第 $k$ 场比赛的排行榜是一个 $n$ 阶排列 $a_k$，表示选手 $a_{k, i}$ 的排名为 $i$。

SolarPea 和 PolarSea 也是选手。SolarPea 想要证明他比 PolarSea 更强。

定义选手 $x$「$l$ - 强于」选手 $y$，当且仅当存在长度为 $l + 1$ 的序列，满足 $b_1 = x$，$b_{l + 1} = y$，且对于所有 $1\leq i\leq l$，均有 $b_i$ 在至少一场比赛中排名小于 $b_{i + 1}$。

给出 $q$ 组询问。在第 $i$ 组询问中，SolarPea 是选手 $x$，PolarSea 是选手 $y$。求出最小的正整数 $l$，使得 $x$「$l$ - 强于」$y$。

$2\leq n\leq 10 ^ 5$，$1\leq q\leq 10 ^ 5$，$1\leq m\leq 5$，$1\leq x, y\leq n$，$x\neq y$。

输入格式

第一行两个整数 $n, m$。

接下来 $m$ 行，每行 $n$ 个整数，表示第 $i$ 场比赛的排行榜。保证 $a_i$ 是 $1, 2, \ldots, n$ 的排列。

接下来一行一个整数 $q$。

接下来 $q$ 行，每行两个整数 $x, y$ 表示一组询问。

输出格式

对于每组询问，输出一行一个整数表示答案。若不存在这样的 $l$，输出 $-1$。

题目描述

There are $n$ contestants and they take part in $m$ contests. You are given the ranklist of each contest. The ranklist of the $k$-th contest is a sequence $a_k$, indicating that the $a_{k, i}$-th contestant’s rank is $i$.

SolarPea and PolarSea are two of the $n$ contestants. SolarPea wants to prove that he is stronger than PolarSea.

Define $x$ is $l$-stronger than $y$, if and only if there exists a sequence $b$ of length $l + 1$, such that $b_1 = x$, $b_{l + 1} = y$, and for all $1\leq i\leq l$, $b_i$ has a smaller rank than $b_{i + 1}$ in at least one contest.

There are $q$ queries. In the $i$-th query, SolarPea is contestant $x$ and PolarSea is contestant $y$. Please find the minimum positive number $l$ such that SolarPea is $l$-stronger than PolarSea.

输入格式

The first line contains two integers $n$ ($2\leq n\leq 10 ^ 5$) and $m$ ($1\leq m\leq 5$).

The $i$-th of the next $m$ lines contains $n$ intergers $a_{i, 1}, a_{i, 2}, \ldots, a_{i, n}$. It is guaranteed that $a_i$ is a permutaion of $1,2,\ldots,n$.

The next line contains an integer $q$ ($1\leq q\leq 10 ^ 5$).

Each of the next $q$ lines contains two integers $x$ and $y$ ($1 \le x,y \le n, x \neq y$), representing a query.

输出格式

For each query, output a number $l$ representing the answer. If there is no legal $l$, output $-1$.

样例 #1

样例输入 #1

1 2 3 4 5 6 7 8

6 2 1 3 2 5 4 6 2 1 4 3 6 5 4 1 4 5 3 6 1 5 2

样例输出 #1

1 2 3 4

1 2 5 3

提示

Source: The 2022 ICPC Asia Xi’an Regional Contest Problem D.

Author: csy2005.

哈希

哈希用于把某个对象通过对其特征的“描述”映射为一个值来进行代表， 用于实现判重/判相等。

比如字符串哈希， 树哈希等等。

字符串哈希

把字符串看成一个$B(B>26)$进制数，计算这个数对某个质数取模的结果作为哈希值。我们随机选取这个$B$和质数$P$。一个结论是两个随机的不同字符串按照这样生成的哈希值相同的概率大约是$\frac 1 P$，所以比较次数很大的时候，我们需要使用两个模数计算两个哈希值，共同作为哈希值使用，这样相同的概率得到减小。

哈希模数表

子串哈希：

令字符串$s$的哈希值为$\sum s_i\times B^{n-i+1}$，那么先求出字符串前缀$f(f_i=f_{i-1}\times B+s_i)$，那么$f_r-f_{l-1}\times B^{r-l+1}$就是子串$[l,r]$的哈希值。

1
2
3
4
5
6
7

pw[0]=1;
for(int i=1;i<=s.size();i++){
    pw[i]=1ll*pw[i-1]*B%P;
}
for(int i=1;i<=s.size();i++){
    f[i]=(1ll*f[i-1]*B+s[i-1])%P;//字符串下标从0开始
}

例题：洛谷 [ABC250E] Prefix Equality

[ABC250E] Prefix Equality

题面翻译

给定两个长为 $N$ 的数列 $A,B$ 与 $Q$ 次询问，每次询问给出 $x_i,y_i$，求出 $A$ 的前 $x_i$ 项去重后是否与 $B$ 的前 $y_i$ 项去重后相同。

题目描述

長さ $ N $ の整数列 $ A\ =\ (a_1,\ldots,a_N) $ と $ B\ =\ (b_1,\ldots,b_N) $ が与えられます。

$ i=1,…,Q $ に対し、次の形式のクエリに答えてください。

• $ A $ の先頭 $ x_i $ 項 $ (a_1,\ldots,a_{x_i}) $ に含まれる値の集合と $ B $ の先頭 $ y_i $ 項 $ (b_1,\ldots,b_{y_i}) $ に含まれる値の集合が等しいならば Yes と、そうでなければ No と出力せよ。

输入格式

入力は以下の形式で標準入力から与えられる。

$ N $ $ a_1 $ $ \ldots $ $ a_N $ $ b_1 $ $ \ldots $ $ b_N $ $ Q $ $ x_1 $ $ y_1 $ $ \vdots $ $ x_Q $ $ y_Q $

输出格式

$ Q $ 行出力せよ。 $ i $ 行目には、$ i $ 番目のクエリに対する出力をせよ。

样例 #1

样例输入 #1

1 2 3 4 5 6 7 8 9 10 11

5 1 2 3 4 5 1 2 2 4 3 7 1 1 2 2 2 3 3 3 4 4 4 5 5 5

样例输出 #1

1 2 3 4 5 6 7

Yes Yes Yes No No Yes No

提示

制約

• $ 1\ \leq\ N,Q\ \leq\ 2\ \times\ 10^5 $
• $ 1\ \leq\ a_i,b_i\ \leq\ 10^9 $
• $ 1\ \leq\ x_i,y_i\ \leq\ N $
• 入力は全て整数

Sample Explanation 1

集合は各値が含まれるかどうかのみに注目した概念であることに気を付けてください。 $ 3 $ 番目のクエリにおいて、$ A $ の先頭 $ 2 $ 項には $ 1 $ と $ 2 $ が $ 1 $ 個ずつ、$ B $ の先頭 $ 3 $ 項には $ 1 $ が $ 1 $ 個と $ 2 $ が $ 2 $ 個含まれます。しかし、それぞれに含まれる値の集合はどちらも $ {\ 1,2\ } $ となり、一致します。 また、$ 6 $ 番目のクエリにおいては各値が現れる順番が異なりますが、やはり集合としては一致します。

分析：

考虑对$A,B$进行哈希。

由于集合的相等与数的顺序无关，所以需要一个交换律运算，考虑使用异或运算。

构造出的哈希函数为：
$$
H(S)=\bigoplus_{s\in S}f(s)
$$
其中$f(s)$是一个数字产生数字的哈希函数，于是有
$$
H(S \cup {x})=\begin{cases}
H(S) & x \in S \
H(S)\oplus f(x) & x \not \in S
\end{cases}
$$
对于每次询问，直接判断即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

#include<bits/stdc++.h>
using namespace std;

const int N=2e5+5,mod=1610612741;

int n,m;
int a[N],b[N];

unordered_set<int>sa,sb;

int f(int x){
    return 1ll*13331*x%mod;
}

int main(){
    cin >> n;
    for(int i=1;i<=n;i++){
        cin >> a[i];
        if(sa.count(a[i])){
            a[i]=a[i-1];
        }
        else{
            sa.insert(a[i]);
            a[i]=a[i-1]^f(a[i]);
        }
    }
    for(int i=1;i<=n;i++){
        cin >> b[i];
        if(sb.count(b[i])){
            b[i]=b[i-1];
        }
        else{
            sb.insert(b[i]);
            b[i]=b[i-1]^f(b[i]);
        }
    }
    cin >> m;
    for(int i=1;i<=m;i++){
        int x,y;
        cin >> x >> y;
        if(a[x]==b[y])cout <<"Yes\n";
        else cout << "No\n";
    }
    return 0;
}

字典树(trie)

支持查询字符串是否出现和插入字符串。

另外，trie可以反映两个字符串之间的前后缀关系。如一个串的结束节点是另外一个串结束节点的祖先， 说明前者是后者的前缀。前后缀的判断可以通过这个性质转化成树上的问题。

例题1：洛谷P3065 [USACO12DEC] First! G

[USACO12DEC] First! G

题目描述

Bessie has been playing with strings again. She found that by

changing the order of the alphabet she could make some strings come before all the others lexicographically (dictionary ordering).

For instance Bessie found that for the strings “omm”, “moo”, “mom”, and “ommnom” she could make “mom” appear first using the standard alphabet and that she could make “omm” appear first using the alphabet

“abcdefghijklonmpqrstuvwxyz”. However, Bessie couldn’t figure out any way to make “moo” or “ommnom” appear first.

Help Bessie by computing which strings in the input could be

lexicographically first by rearranging the order of the alphabet. To compute if string X is lexicographically before string Y find the index of the first character in which they differ, j. If no such index exists then X is lexicographically before Y if X is shorter than Y. Otherwise X is lexicographically before Y if X[j] occurs earlier in the alphabet than Y[j].

Bessie一直在研究字符串。她发现，通过改变字母表的顺序，她可以按改变后的字母表来排列字符串（字典序大小排列）。

例如，Bessie发现，对于字符串串“omm”，“moo”，“mom”和“ommnom”，她可以使用标准字母表使“mom”排在第一个（即字典序最小），她也可以使用字母表“abcdefghijklonmpqrstuvwxyz”使得“omm”排在第一个。然而，Bessie想不出任何方法（改变字母表顺序）使得“moo”或“ommnom”排在第一个。

接下来让我们通过重新排列字母表的顺序来计算输入中有哪些字符串可以排在第一个（即字典序最小），从而帮助Bessie。

要计算字符串X和字符串Y按照重新排列过的字母表顺序来排列的顺序，先找到它们第一个不同的字母X[i]与Y[i]，按重排后的字母表顺序比较，若X[i]比Y[i]先，则X的字典序比Y小，即X排在Y前；若没有不同的字母，则比较X与Y长度，若X比Y短，则X的字典序比Y小，即X排在Y前。

输入格式

* Line 1: A single line containing N (1 <= N <= 30,000), the number of strings Bessie is playing with.

* Lines 2..1+N: Each line contains a non-empty string. The total number of characters in all strings will be no more than 300,000. All characters in input will be lowercase characters ‘a’ through ‘z’. Input will contain no duplicate strings.

第1行：一个数字N（1 <= N <= 30,000），Bessie正在研究的字符串的数量。

第2N+1行：每行包含一个非空字符串。所有字符串包含的字符总数不会超过300,000。 输入中的所有字符都是小写字母，即az。 输入不包含重复的字符串。

输出格式

* Line 1: A single line containing K, the number of strings that could be lexicographically first.

* Lines 2..1+K: The (1+i)th line should contain the ith string that could be lexicographically first. Strings should be output in the same order they were given in the input.

第1行：一个数字K，表示按重排后的字母表顺序排列的字符串有多少可以排在第一个数量。

第2~K+1行：第i+1行包含第i个按重排后的字母表顺序排列后可以排在第一个的字符串。字符串应该按照它们在输入中的顺序来输出。

样例 #1

样例输入 #1

1 2 3 4 5

4 omm moo mom ommnom

样例输出 #1

1 2 3

2 omm mom

提示

The example from the problem statement.

Only “omm” and “mom” can be ordered first.

样例即是题目描述中的例子，只有“omm”和“mom”在各自特定的字典序下可以被排列在第一个。

分析：

考虑到字典序比大小只和第一个不相同的字符有关，联想到可以在Trie树上做这个事情。

分情况讨论， 对26个字母连边表示如果要当前串字典序最小，这些字母应该满足什么要求即可。

考虑拿着这个串在Trie上走， 那么走到当前位置以后，因为要求当前串最小，所以要对同一层的其余子树里面有串的字符连边，表示当前字母小，这样可以得到一个有向图，判断这个有向图有没有环就可以判断有没有矛盾。

这样我们考虑了所有没有前后缀关系的串，对于有前后缀关系的串，如果一个串的终止节点的祖先中存在别的串终止节点，这个串一定不是最小串。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

#include<bits/stdc++.h>
using namespace std;

const int N=3e4+5,M=3e5+5;
int n;
string s[N];
int trie[M][30];
int cnt[M];
int idx;
void insert(string str){
    int now=0;
    for(int i=0;i<str.length();i++){
        if(!trie[now][str[i]-'a']){
            trie[now][str[i]-'a']=++idx;
        }
        now=trie[now][str[i]-'a'];
    }
    cnt[now]++;
}
int d[30];
int h[30],ne[30*M],to[30*M],eidx;

void addedge(int u,int v){
    ne[++eidx]=h[u];
    h[u]=eidx;
    to[eidx]=v;
    d[v]++;
}

bool check(string str){
    memset(d,0,sizeof d);
    memset(h,0,sizeof h);
    eidx=0;
    int now=0;
    for(int i=0;i<str.length();i++){
        if(cnt[now])return 0;
        for(int j=0;j<26;j++){
            if(trie[now][j]&&j!=str[i]-'a'){
                addedge(str[i]-'a',j);
            }
        }
        now=trie[now][str[i]-'a'];
    }
    queue<int>q;
    while(!q.empty()){
        q.pop();
    }
    for(int i=0;i<26;i++){
        if(d[i]==0)q.push(i);
    }
    while(!q.empty()){
        int t=q.front();
        q.pop();
        for(int i=h[t];i;i=ne[i]){
            d[to[i]]--;
            if(d[to[i]]==0)q.push(to[i]);
        }
    }
    for(int i=0;i<26;i++){
        if(d[i])return 0;
    }
    return 1;
}

int ans;
bool out[N];

int main(){
    cin >> n;
    for(int i=1;i<=n;i++){
        cin >> s[i];
        insert(s[i]);
    }
    for(int i=1;i<=n;i++){
        if(check(s[i])){
            ans++;
            out[i]=1;
        }
    }
    cout << ans << endl;
    for(int i=1;i<=n;i++){
        if(out[i])cout << s[i] << endl;
    }
    return 0;
}

例题2：洛谷P4551 最长异或路径

最长异或路径

题目描述

给定一棵 $n$ 个点的带权树，结点下标从 $1$ 开始到 $n$。寻找树中找两个结点，求最长的异或路径。

异或路径指的是指两个结点之间唯一路径上的所有边权的异或。

输入格式

第一行一个整数 $n$，表示点数。

接下来 $n-1$ 行，给出 $u,v,w$ ，分别表示树上的 $u$ 点和 $v$ 点有连边，边的权值是 $w$。

输出格式

一行，一个整数表示答案。

样例 #1

样例输入 #1

1 2 3 4

4 1 2 3 2 3 4 2 4 6

样例输出 #1

1

7

提示

最长异或序列是 $1,2,3$，答案是 $7=3\oplus 4$。

数据范围

$1\le n \le 100000;0 < u,v \le n;0 \le w < 2^{31}$。

例题3：洛谷CF888G Xor-MST

Xor-MST

题面翻译

• 给定 $n$ 个结点的无向完全图。每个点有一个点权为 $a_i$。连接 $i$ 号结点和 $j$ 号结点的边的边权为 $a_i\oplus a_j$。
• 求这个图的 MST 的权值。
• $1\le n\le 2\times 10^5$，$0\le a_i< 2^{30}$。

题目描述

You are given a complete undirected graph with $ n $ vertices. A number $ a_{i} $ is assigned to each vertex, and the weight of an edge between vertices $ i $ and $ j $ is equal to $ a_{i}xora_{j} $ .

Calculate the weight of the minimum spanning tree in this graph.

输入格式

The first line contains $ n $ ( $ 1<=n<=200000 $ ) — the number of vertices in the graph.

The second line contains $ n $ integers $ a_{1} $ , $ a_{2} $ , …, $ a_{n} $ ( $ 0<=a_{i}<2^{30} $ ) — the numbers assigned to the vertices.

输出格式

Print one number — the weight of the minimum spanning tree in the graph.

样例 #1

样例输入 #1

1 2	5 1 2 3 4 5

样例输出 #1

1

8

样例 #2

样例输入 #2

1 2

4 1 2 3 4

样例输出 #2

1

8

KMP

KMP是最经典的字符串算法之一。

用于解决字符串匹配问题，可以求出自身每个前缀的最长border。

border：既是前缀又是后缀的非本身的子串

例题1：洛谷P5829 【模板】失配树

【模板】失配树

题目描述

给定一个字符串 $s$，定义它的 $k$ 前缀 $\mathit{pre}k$ 为字符串 $s{1\dots k}$，**$k$ 后缀** $\mathit{suf}k$ 为字符串 $s{|s|-k+1\dots |s|}$，其中 $1 \le k \le |s|$。

定义 $\bold{Border}(s)$ 为对于 $i \in [1, |s|)$，满足 $\mathit{pre}_i = \mathit{suf}_i$ 的字符串 $\mathit{pre}_i$ 的集合。$\bold{Border}(s)$ 中的每个元素都称之为字符串 $s$ 的 $\operatorname{border}$。

有 $m$ 组询问，每组询问给定 $p,q$，求 $s$ 的 $\boldsymbol{p}$ 前缀 和 $\boldsymbol{q}$ 前缀 的 最长公共 $\operatorname{border}$ 的长度。

输入格式

第一行一个字符串 $s$。

第二行一个整数 $m$。

接下来 $m$ 行，每行两个整数 $p,q$。

输出格式

对于每组询问，一行一个整数，表示答案。若不存在公共 $\operatorname{border}$，请输出 $0$。

样例 #1

样例输入 #1

1 2 3 4 5 6 7

aaaabbabbaa 5 2 4 7 10 3 4 1 2 4 11

样例输出 #1

1 2 3 4 5

1 1 2 0 2

样例 #2

样例输入 #2

1 2 3 4 5

zzaaccaazzccaacczz 3 2 18 10 18 3 5

样例输出 #2

1 2 3

1 2 0

提示

样例 $2$ 说明：

对于第一个询问，$2$ 前缀和 $18$ 前缀分别是 zz 和 zzaaccaazzccaacczz，由于 zz 只有一个 $\operatorname{border}$，即 z，故最长公共 $\operatorname{border}$ 长度为 $1$。

---

对于 $16%$ 的数据，$s$ 中的字符全部相等。

对于 $100%$ 的数据，$1\leq p,q \le |s|\leq 10^6$，$1 \leq m \leq 10^5$，$s_i \in [\texttt{a}, \texttt{z}]$

分析：

先给出一个border的性质。

$S[1\cdots i]$ 的所有border由 $next[S\cdots i]], next[next[S[1\cdots i]]], next[next[next[S[1\cdots i]]]], \cdots$ 等给出。 其中 $next[i]$ 是 $i$ 这个位置的最长border数组。

考虑 $next[i]$ 是 $i$ 最长的border， 那么 $i$ 剩下的border一定比 $next[i]$ 短， 且一定是 $next[i]$ 的border。

那么把$ i \to next[i]$ 建边这就是一棵树， 公共最长border就是 LCA 。 写一个求 LCA 即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

#include<bits/stdc++.h>
using namespace std;

const int N=1e6+5;

string s;
int n,m;
int nxt[N];

int h[N],ne[N],to[N];
int idx;
int fa[N][21],d[N];
void addedge(int u,int v){
    ne[++idx]=h[u];
    h[u]=idx;
    to[idx]=v;
    fa[v][0]=u;
    d[v]=d[u]+1;
}

void init(){
    for(int i=1;i<=20;i++){
        for(int j=1;j<=n;j++){
            fa[j][i]=fa[fa[j][i-1]][i-1];
        }
    }
}

int lca(int x,int y){
    if(d[x]<d[y])swap(x,y);
    if(d[x]!=d[y]){
        for(int i=20;i>=0;i--){
            if(d[fa[x][i]]>=d[y])x=fa[x][i];
        }
    }
    if(x==y)return x;
    for(int i=20;i>=0;i--){
        if(fa[x][i]!=fa[y][i]){
            x=fa[x][i],y=fa[y][i];
        }
    }
    return fa[x][0];
}

int main(){
    cin >> s;
    n=s.length();
    s=" "+s;
    for(int i=2,j=0;i<=n;i++){
        while(j&&s[i]!=s[j+1])j=nxt[j];
        if(s[i]==s[j+1])j++;
        nxt[i]=j;
    }
    for(int i=1;i<=n;i++){
        addedge(nxt[i],i);
    }
    init();
    
    cin >> m;
    for(int i=1;i<=m;i++){
        int x,y;
        cin >> x >> y;
        cout << lca(nxt[x],nxt[y]) << endl;
    }
    return 0;
}

例题2：洛谷P3193 [HNOI2008] GT考试

[HNOI2008] GT考试

题目描述

阿申准备报名参加 GT 考试，准考证号为 $N$ 位数$X_1,X_2…X_n\ (0\le X_i\le 9)$，他不希望准考证号上出现不吉利的数字。
他的不吉利数字$A_1,A_2,\cdots, A_m\ (0\le A_i\le 9)$ 有 $M$ 位，不出现是指 $X_1,X_2\cdots X_n$ 中没有恰好一段等于 $A_1,A_2,\cdots ,A_m$，$A_1$ 和 $X_1$ 可以为 $0$。

输入格式

第一行输入 $N,M,K$ 接下来一行输入 $M$ 位的数。

输出格式

阿申想知道不出现不吉利数字的号码有多少种，输出模 $K$ 取余的结果。

样例 #1

样例输入 #1

1 2	4 3 100 111

样例输出 #1

1

81

提示

数据范围及约定

对于全部数据，$N\leq10^9$，$M\leq 20$，$K\leq1000$。

离散化

对于某些问题，我们往往只需考虑一些关键值以及其附近的值。

例题1：洛谷 CF930E Coins Exhibition

Coins Exhibition

题面翻译

题目大意

有$k(1 \leq k \leq 10^9)$个硬币，每个硬币有正面朝上和反面朝上两种状态。

现有$n+m(0 \leq n,m \leq 10^5)$个限制条件，每个限制条件形如$(l_i,r_i)(1 \leq l_i \leq r_i \leq k)$。前$n$个限制条件限制区间$[l_i,r_i]$内至少有一个硬币正面朝上，后$m$个限制条件限制区间$[l_i,r_i]$内至少有一个硬币反面朝上。

问共有多少种摆放硬币的方案使得所有限制条件都被满足。答案对$10^9+7$取模。

输入数据格式

第一行三个整数$k,n,m$

接下来$n+m$行每行两个正整数$l_i,r_i$表示一个限制区间

输出数据格式

一行表示方案数

题目描述

Arkady and Kirill visited an exhibition of rare coins. The coins were located in a row and enumerated from left to right from $ 1 $ to $ k $ , each coin either was laid with its obverse (front) side up, or with its reverse (back) side up.

Arkady and Kirill made some photos of the coins, each photo contained a segment of neighboring coins. Akrady is interested in obverses, so on each photo made by him there is at least one coin with obverse side up. On the contrary, Kirill is interested in reverses, so on each photo made by him there is at least one coin with its reverse side up.

The photos are lost now, but Arkady and Kirill still remember the bounds of the segments of coins each photo contained. Given this information, compute the remainder of division by $ 10^{9}+7 $ of the number of ways to choose the upper side of each coin in such a way, that on each Arkady’s photo there is at least one coin with obverse side up, and on each Kirill’s photo there is at least one coin with reverse side up.

输入格式

The first line contains three integers $ k $ , $ n $ and $ m $ ( $ 1<=k<=10^{9} $ , $ 0<=n,m<=10^{5} $ ) — the total number of coins, the number of photos made by Arkady, and the number of photos made by Kirill, respectively.

The next $ n $ lines contain the descriptions of Arkady’s photos, one per line. Each of these lines contains two integers $ l $ and $ r $ ( $ 1<=l<=r<=k $ ), meaning that among coins from the $ l $ -th to the $ r $ -th there should be at least one with obverse side up.

The next $ m $ lines contain the descriptions of Kirill’s photos, one per line. Each of these lines contains two integers $ l $ and $ r $ ( $ 1<=l<=r<=k $ ), meaning that among coins from the $ l $ -th to the $ r $ -th there should be at least one with reverse side up.

输出格式

Print the only line — the number of ways to choose the side for each coin modulo $ 10^{9}+7=1000000007 $ .

样例 #1

样例输入 #1

1 2 3 4 5

5 2 2 1 3 3 5 2 2 4 5

样例输出 #1

1

8

样例 #2

样例输入 #2

1 2 3 4 5 6

5 3 2 1 3 2 2 3 5 2 2 4 5

样例输出 #2

1

0

样例 #3

样例输入 #3

1 2 3 4 5 6 7 8 9 10 11 12 13

60 5 7 1 3 50 60 1 60 30 45 20 40 4 5 6 37 5 18 50 55 22 27 25 31 44 45

样例输出 #3

1

732658600

提示

In the first example the following ways are possible (‘O’ — obverse, ‘R’ — reverse side):

• OROOR,
• ORORO,
• ORORR,
• RROOR,
• RRORO,
• RRORR,
• ORROR,
• ORRRO.

In the second example the information is contradictory: the second coin should have obverse and reverse sides up at the same time, that is impossible. So, the answer is $ 0 $ .

分析：

首先可以得到一个$O(k+n+m)$的做法。

我们对于每个位置$i$求出，在$i$之前（包括$i$）至多能填多少个$1$，那么可以dp，记$f_{i,0/1}$表示考虑了前$i$个位置，上个位置选的$0/1$合法得到方案数，枚举最后一个相同段的长度（最后一个不同位）即可转移，容易使用前缀和优化至线性。

注意到我们可以将所有$l_i,r_i+1$离散化，将值域划分成若干以关键点作为左端点的区间，那么题中所有$[l_i,r_i]$会对应的到离散化后一段区间的并。

于是我们可以从前往后一段段区间考虑，记$f_{i,0/1/2}$表示考虑了前$i$段区间，上一个位置全$0$，全$1$，或是$01$交替的方案数，前两者的转移类似，$01$交替时我们直接满足了所有要考虑的限制，$f_{i,2} \gets (2^{len_i}-2)(f_{i-1,0}+f_{i-1,1}+f_{i-1,2})$即可。

复杂度$O((n+m)\log(n+m))$，瓶颈在于排序与快速幂（可用基数排序+快速幂做到线性）。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+5,mod=1e9+7;
typedef long long ll;
ll k,n,m;

ll all[4*N];
ll cnt;
ll find(ll x){
    ll l=0,r=cnt;
    while(l<r){
        ll mid=l+r>>1;
        if(x<=all[mid])r=mid;
        else l=mid+1;
    }
    return l;
}

long long qkpow(ll x,ll k){
    long long a=1;
    while(k){
        if(k&1)a=a*x%mod;
        x=x*x%mod;
        k>>=1;
    }
    return a%mod;
}

pair<ll,ll>a1[N],a2[N];
ll minn[2][4*N];//枚举最后一个相同串的长度->求最后一个不同值的位置
long long f[4*N][3];
int main(){
    cin >> k >> n >> m;
    for(ll i=1;i<=n;i++){
        ll l,r;
        cin >> l >> r;
        l--;
        all[++cnt]=l,all[++cnt]=r;
        a1[i]={l,r};
    }
    for(ll i=1;i<=m;i++){
        ll l,r;
        cin >> l >> r;
        l--;
        all[++cnt]=l,all[++cnt]=r;
        a2[i]={l,r};
    }
    all[++cnt]=k;
    sort(all+1,all+cnt+1);
    cnt=unique(all,all+cnt+1)-(all+1);
    for(ll i=0;i<=cnt;i++){
        minn[0][i]=minn[1][i]=cnt+1;
    }
    for(ll i=1;i<=n;i++){
        ll l=find(a1[i].first),r=find(a1[i].second);
        minn[0][l]=min(minn[0][l],r);
    }
    for(ll i=1;i<=m;i++){
        ll l=find(a2[i].first),r=find(a2[i].second);
        minn[1][l]=min(minn[1][l],r);
    }
    for(ll i=cnt;i;i--){
        minn[0][i-1]=min(minn[0][i],minn[0][i-1]);
        minn[1][i-1]=min(minn[1][i],minn[1][i-1]);
    }
    f[cnt][0]=f[cnt][1]=f[cnt][2]=1;
    for(ll i=cnt-1;i>=0;i--){
        f[i][0]=(f[i+1][0]+f[i+1][1]-f[minn[1][i]][1]+f[i+1][2]*(qkpow(2,all[i+1]-all[i])-2)%mod)%mod;
        f[i][1]=(f[i+1][1]+f[i+1][0]-f[minn[0][i]][0]+f[i+1][2]*(qkpow(2,all[i+1]-all[i])-2)%mod)%mod;
        f[i][2]=(f[i+1][0]-f[minn[0][i]][0]+f[i+1][1]-f[minn[1][i]][1]+f[i+1][2]*(qkpow(2,all[i+1]-all[i])-2)%mod)%mod;
    }
    cout << (f[0][2]+mod)%mod;
    return 0;
}

例题2：洛谷 CF1835B Lottery

Lottery

题面翻译

简要题意：

给定一个长度为 $n$ 的序列 $v$，其值域为 $[0,m]$。

现在你需要选择一个 $x \in [0,m]$，使其权值最大。定义一个数 $x$ 的权值为：

$$\sum_{c=0}^{m}[\sum_{i=1}^{n}[\vert v_i - c \vert \leq \vert x - c \vert] < k]$$

请你找到权值最大的数 $x$，若有多个，输出最小的那个。

Translated by Demeanor_Roy

题目描述

$ n $ people indexed with integers from $ 1 $ to $ n $ came to take part in a lottery. Each received a ticket with an integer from $ 0 $ to $ m $ .

In a lottery, one integer called target is drawn uniformly from $ 0 $ to $ m $ . $ k $ tickets (or less, if there are not enough participants) with the closest numbers to the target are declared the winners. In case of a draw, a ticket belonging to the person with a smaller index is declared a winner.

Bytek decided to take part in the lottery. He knows the values on the tickets of all previous participants. He can pick whatever value he wants on his ticket, but unfortunately, as he is the last one to receive it, he is indexed with an integer $ n + 1 $ .

Bytek wants to win the lottery. Thus, he wants to know what he should pick to maximize the chance of winning. He wants to know the smallest integer in case there are many such integers. Your task is to find it and calculate his chance of winning.

输入格式

In the first line of the input, there are the integers $ n $ , $ m $ , and $ k $ ( $ 1 \leq n \leq 10^6 $ , $ 0 \leq m \leq 10^{18} $ , $ 1 \leq k \leq 10^6 $ ).

In the following line, there are $ n $ integers separated by a single space, denoting the numbers on tickets received by people participating in a lottery. These numbers are integers in the range from $ 0 $ to $ m $ .

输出格式

You should output two integers separated by a single space on the standard output. The first should be equal to the number of target values (from $ 0 $ to $ m $ ), upon drawing which Baytek wins, given that he chooses his ticket optimally. The second should be equal to the integer Bytek should pick to maximize his chance of winning the lottery.

样例 #1

样例输入 #1

1 2	3 6 2 1 4 5

样例输出 #1

1

4 2

样例 #2

样例输入 #2

1 2	7 7 1 2 4 7 3 0 1 6

样例输出 #2

1

1 5

提示

In the first example, Bytek wins for $ 4 $ target values (namely $ 0, 1, 2, 3 $ ) if he chooses integer $ 2 $ , which is the lowest optimal value. If he chooses $ 3 $ , he also wins in four cases, but it is not the lowest value.

启发式合并

启发式合并大致解决一类有向信息合并问题。具体地，我们需要支持动态将集合$S$合并至集合$T$（之后就再也用不到集合$S$了）这一类操作。

我们用某种数据结构维护集合，合并时若$S$的大小小于$T$的大小，就暴力枚举$S$内的元素加入$T$中，否则直接交换这两个数据结构，再暴力枚举$S$内的元素加入$T$中。

大部分数据结构的交换都是$O(1)$的，若不能高效交换我们可以认为记录每个集合的编号，交换两个集合编号即可。

考虑如何记录复杂度，一个点被暴力插入另一个集合后所在的集合大小总会翻倍，因此其只会被操作$O(\log n)$次，因此总插入次数$O(n\log n)$。

例题1：洛谷P8907 [USACO22DEC] Making Friends P

[USACO22DEC] Making Friends P

题目描述

FJ 的 $N(2 \le N \le 2 \times 10^5)$ 头编号为 $1 \cdots N$ 的奶牛之中初始时有 $M(1 \le M \le 2 \times 10^5)$ 对朋友。奶牛们一头一头地离开农场去度假。第 $i$ 天，第 $i$ 头奶牛离开了农场，同时第 $i$ 头奶牛的所有仍在农场的朋友互相都成为了朋友。问总共建立了多少新的朋友关系？

输入格式

输入的第一行包含 $N$ 和 $M$。

以下 $M$ 行每行包含两个整数 $u_i$ 和 $v_i$，表示奶牛 $u_i$ 和 $v_i$ 是朋友（$1 \le u_i,v_i \le N,u_i \neq v_i$）。每个奶牛无序对至多出现一次。

输出格式

输出一行，包含形成的新的朋友关系的总数。不要计入初始时已经是朋友的奶牛对。

样例 #1

样例输入 #1

1 2 3 4 5 6 7

>7 6 >1 3 >1 4 >7 1 >2 3 >2 4 >3 5

样例输出 #1

1

>5

提示

样例 1 解释

第 $1$ 天，三个新的朋友关系被建立：$(3,4)$，$(3,7)$ 和 $(4,7)$。

第 $3$ 天，两个新的朋友关系被建立：$(4,5)$ 和 $(5,7)$。

测试点性质

• 测试点 $2-3$ 满足 $N \le 500$。
• 测试点 $4-7$ 满足 $N \le 10^4$。
• 测试点 $8-17$ 没有额外限制。

分析：

考虑一个性质，每次互相连边显然有些多余，不妨转化成将编号最小的点和其它点连边。

考虑正确性，若一头牛$x$出队，不妨设与他相连且编号大于他的牛的编号排序后的结果为 $y_1,y_2,\cdots,y_k$，我们这种连边策略相当于延时连边，即在$y_1$出队以前连接$y_1 \to y_2,y_3,\cdots$ ，$y_2$出队以前连接$y_2 \to y_3,\cdots$，每条应当连的边都被连上了至少一次，故存在充分性，所以正确。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

#include<bits/stdc++.h>
using namespace std;

const int N=2e5+5;
int n,m;
set<int>s[N];

long long ans;
int main(){
    cin >> n >> m;
    for(int i=1;i<=m;i++){
        int u,v;
        cin >> u >> v;
        s[min(u,v)].insert(max(u,v));
    }
    for(int i=1;i<=n;i++){
        if(s[i].empty())continue;
        ans+=s[i].size();
        int t=*s[i].begin();
        s[i].erase(s[i].begin());
        if(s[i].size()>s[t].size())swap(s[i],s[t]);
        for(auto x:s[i]){
            s[t].insert(x);
        }
    }
    cout << ans-m << endl;
    return 0;
}

例题2：[洛谷CF1416D Graph and Queries](Graph and Queries - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))

Graph and Queries

题面翻译

给定一个 $n$ 个点 $m$ 条边的无向图，第 $i$ 个点的点权初始值为 $p_i$,所有 $p_i$ 互不相同。

接下来进行 $q$ 次操作，分为两类：

• $\tt 1\ v$ 查询与 $v$ 连通的点中， $p_u$ 最大的点 $u$ 并输出 $p_u$，然后让 $p_u=0$。
• $\tt 2\ i$ 将第 $i$ 条边删掉。

翻译者：一只书虫仔

题目描述

You are given an undirected graph consisting of $ n $ vertices and $ m $ edges. Initially there is a single integer written on every vertex: the vertex $ i $ has $ p_i $ written on it. All $ p_i $ are distinct integers from $ 1 $ to $ n $ .

You have to process $ q $ queries of two types:

• $ 1 $ $ v $ — among all vertices reachable from the vertex $ v $ using the edges of the graph (including the vertex $ v $ itself), find a vertex $ u $ with the largest number $ p_u $ written on it, print $ p_u $ and replace $ p_u $ with $ 0 $ ;
• $ 2 $ $ i $ — delete the $ i $ -th edge from the graph.

Note that, in a query of the first type, it is possible that all vertices reachable from $ v $ have $ 0 $ written on them. In this case, $ u $ is not explicitly defined, but since the selection of $ u $ does not affect anything, you can choose any vertex reachable from $ v $ and print its value (which is $ 0 $ ).

输入格式

The first line contains three integers $ n $ , $ m $ and $ q $ ( $ 1 \le n \le 2 \cdot 10^5 $ ; $ 1 \le m \le 3 \cdot 10^5 $ ; $ 1 \le q \le 5 \cdot 10^5 $ ).

The second line contains $ n $ distinct integers $ p_1 $ , $ p_2 $ , …, $ p_n $ , where $ p_i $ is the number initially written on vertex $ i $ ( $ 1 \le p_i \le n $ ).

Then $ m $ lines follow, the $ i $ -th of them contains two integers $ a_i $ and $ b_i $ ( $ 1 \le a_i, b_i \le n $ , $ a_i \ne b_i $ ) and means that the $ i $ -th edge connects vertices $ a_i $ and $ b_i $ . It is guaranteed that the graph does not contain multi-edges.

Then $ q $ lines follow, which describe the queries. Each line is given by one of the following formats:

• $ 1 $ $ v $ — denotes a query of the first type with a vertex $ v $ ( $ 1 \le v \le n $ ).
• $ 2 $ $ i $ — denotes a query of the second type with an edge $ i $ ( $ 1 \le i \le m $ ). For each query of the second type, it is guaranteed that the corresponding edge is not deleted from the graph yet.

输出格式

For every query of the first type, print the value of $ p_u $ written on the chosen vertex $ u $ .

样例 #1

样例输入 #1

1 2 3 4 5 6 7 8 9 10 11 12

5 4 6 1 2 5 4 3 1 2 2 3 1 3 4 5 1 1 2 1 2 3 1 1 1 2 1 2

样例输出 #1

1 2 3 4

5 1 2 0

分析：

倒序处理，删边可以变为加边，直接进行启发式合并即可，但是操作1强制在线，不能直接做。

我们将启发式合并的结构离线，记录下形如“将某个集合全部加入另一个集合”的信息，倒序处理后我们便知道一次操作应当将集合内的哪些元素分裂出来，于是就可以在线性处理。

使用set维护每个连通块，删除时暴力删除即可，复杂度$O(n\log ^2 n)$，不能通过本题。

考虑使用vector，在里面存下所有连通块内的值，初始我们令整个vector有序，之后我们对于每个点打上属于某个连通块的标记，相当于在之前的块中删除，这样就可以类似两个优先队列支持删除。

复杂度$O(n\log n)$。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5;
int n,m,q;
vector<int>v[N];
int a[N];
int mu[N],mv[N];//记录边
int qo[N],qx[N],r[N];//记录询问
int bel[N],used[N];//记录属于哪个连通块和是否已经被删除
int del[N];//记录边是否被删除
int fa[N],sz[N];//并查集
int find(int x){
    return (x==fa[x])?x:find(fa[x]);
}

int merge(int x,int y){
    x=find(x),y=find(y);
    if(x==y)return 0;
    if(sz[x]<sz[y])swap(x,y);
    sz[x]+=sz[y];
    for(auto t:v[y])v[x].push_back(t);
    fa[y]=x;
    return y;
}

int get(int x){
    while(v[x].size()&&(bel[v[x].back()]!=x||used[v[x].back()])){//找到最大的属于连通块的没被删除的点
        v[x].pop_back();
    }
    if(!v[x].size())return 0;//没找到
    int t=v[x].back();
    used[t]=1;//标记删除
    v[x].pop_back();
    return t;
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    cin >> n >> m >> q;
    for(int i=1;i<=n;i++){
        cin >> a[i];
        v[i].push_back(a[i]);
        fa[i]=i,sz[i]=1;
    }
    for(int i=1;i<=m;i++){
        cin >> mu[i] >> mv[i];
    }
    for(int i=1;i<=q;i++){
        cin >> qo[i] >> qx[i];
        if(qo[i]==2)del[qx[i]]=1;//记录删除的边
    }
    for(int i=1;i<=m;i++){//连接没被删除过的边
        if(del[i])continue;
        merge(mu[i],mv[i]);
    }
    for(int i=q;i>=1;i--){//逆序处理连边
        int x=find(mu[qx[i]]),y=find(mv[qx[i]]);
        if(qo[i]==1||x==y)continue;
        r[i]=merge(x,y);//记录每次操作后被合并到其他连通块的连通块编号
    }
    for(int i=1;i<=n;i++){//排序，记录值属于哪个连通块
        sort(v[i].begin(),v[i].end());
        bel[a[i]]=find(i);
    }
    for(int i=1;i<=q;i++){
        if(qo[i]==1)cout << get(find(qx[i])) << endl;
        else if(r[i]){//删边
            for(auto x:v[r[i]])bel[x]=r[i];//将这次操作原来不属于当前连通块的点还原
            fa[r[i]]=r[i];
        }
    }
    return 0;
}

扫描线

To Be Update

搜索

例题1：洛谷[ABC252Ex] K-th beautiful Necklace

[ABC252Ex] K-th beautiful Necklace

题面翻译

给定 $ n $ 个珠子，每个珠子的颜色为 $ d_i $，权值为 $ v_i $。颜色共有 $ c $ 种，且保证每种颜色至少有一颗珠子。你需要从 $ n $ 个珠子种选择 $ c $ 个颜色不同的珠子串成一条项链，其权值为其中所有珠子权值的异或和。你需要输出权值第 $ k $ 大的项链的权值。只要选取的珠子不同，即使权值相同也算不同项链。数据保证可能构成的项链数不小于 $ k $。

题目描述

$ N $ 個の宝石があります。$ i $ 番目の宝石は色が $ D_i $ で美しさが $ V_i $ です。
ここで、色は $ 1,2,\ldots,C $ のいずれかであり、どの色の宝石も少なくとも $ 1 $ 個存在します。

$ N $ 個の宝石から、色が相異なる $ C $ 個の宝石を選んでネックレスを作ります。（選ぶ順番は考えません。） ネックレスの美しさは選んだ宝石の美しさのビットごとの $ \rm\ XOR $ となります。

全てのありえるネックレスの作り方のうち、美しさが $ K $ 番目に大きいもののネックレスの美しさを求めてください。（同じ美しさの作り方が複数存在する場合、それらは全て数えます。）

ビットごとの $ \rm\ XOR $ とは 整数 $ A,\ B $ のビットごとの $ \rm\ XOR $ 、$ A\ {\rm\ XOR}\ B $ は、以下のように定義されます。 - $ A\ {\rm\ XOR}\ B $ を二進表記した際の $ 2^k $ ($ k\ \geq\ 0 $) の位の数は、$ A,\ B $ を二進表記した際の $ 2^k $ の位の数のうち一方のみが $ 1 $ であれば $ 1 $、そうでなければ $ 0 $ である。

例えば、$ 3\ {\rm\ XOR}\ 5\ =\ 6 $ となります (二進表記すると: $ 011\ {\rm\ XOR}\ 101\ =\ 110 $)。

输入格式

入力は以下の形式で標準入力から与えられる。

$ N $ $ C $ $ K $ $ D_1 $ $ V_1 $ $ \vdots $ $ D_N $ $ V_N $

输出格式

答えを出力せよ。

样例 #1

样例输入 #1

1 2 3 4 5

4 2 3 2 4 2 6 1 2 1 3

样例输出 #1

1

5

样例 #2

样例输入 #2

1 2 3 4

3 1 2 1 0 1 0 1 0

样例输出 #2

1

0

样例 #3

样例输入 #3

1 2 3 4 5 6 7 8 9 10 11

10 3 11 1 414213562373095048 1 732050807568877293 2 236067977499789696 2 449489742783178098 2 645751311064590590 2 828427124746190097 3 162277660168379331 3 316624790355399849 3 464101615137754587 3 605551275463989293

样例输出 #3

1	766842905529259824

提示

制約

• $ 1\ \leq\ C\ \leq\ N\ \leq\ 70 $
• $ 1\ \leq\ D_i\ \leq\ C $
• $ 0\ \leq\ V_i\ <\ 2^{60} $
• $ 1\ \leq\ K\ \leq\ 10^{18} $
• 少なくとも $ K $ 種類のネックレスを作ることができる
• 入力に含まれる値は全て整数である

Sample Explanation 1

以下のような $ 4 $ 種類のネックレスを作ることができます。 - $ 1,3 $ 番目の宝石を選ぶ。ネックレスの美しさは $ 4\ {\rm\ XOR}\ 2\ =6 $ となる。 - $ 1,4 $ 番目の宝石を選ぶ。ネックレスの美しさは $ 4\ {\rm\ XOR}\ 3\ =7 $ となる。 - $ 2,3 $ 番目の宝石を選ぶ。ネックレスの美しさは $ 6\ {\rm\ XOR}\ 2\ =4 $ となる。 - $ 2,4 $ 番目の宝石を選ぶ。ネックレスの美しさは $ 6\ {\rm\ XOR}\ 3\ =5 $ となる。 よって美しさが $ 3 $ 番目に大きいネックレスの美しさは $ 5 $ となります。

Sample Explanation 2

$ 3 $ 種類のネックレスを作ることができ、いずれも美しさは $ 0 $ です。