堆
操作:
- 插入一个数
- 求集合中的最大(小)值
- 删除集合的最大(小)值
- 删除任意一个元素
- 修改任意一个元素
以下以小根堆(根节点为最小值为例)
基本结构:二叉树
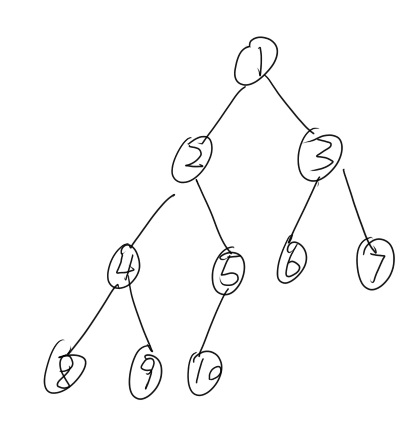
存储:用一个数组$heap$存储二叉树,$size$表示数组中元素的个数,$heap[1]$为根节点,对于一个节点$i$,$i2$是它的左儿子,$i2+1$是它的右儿子。
性质:对于每一个非根节点,它的值一定大于其父节点值
例:

此时的$heap$数组:
| $i$ |
$1$ |
$2$ |
$3$ |
$4$ |
$5$ |
$6$ |
$7$ |
$8$ |
$9$ |
$10$ |
| $heap[i]$ |
$1$ |
$2$ |
$3$ |
$4$ |
$5$ |
$6$ |
$7$ |
$8$ |
$9$ |
$10$ |
操作:
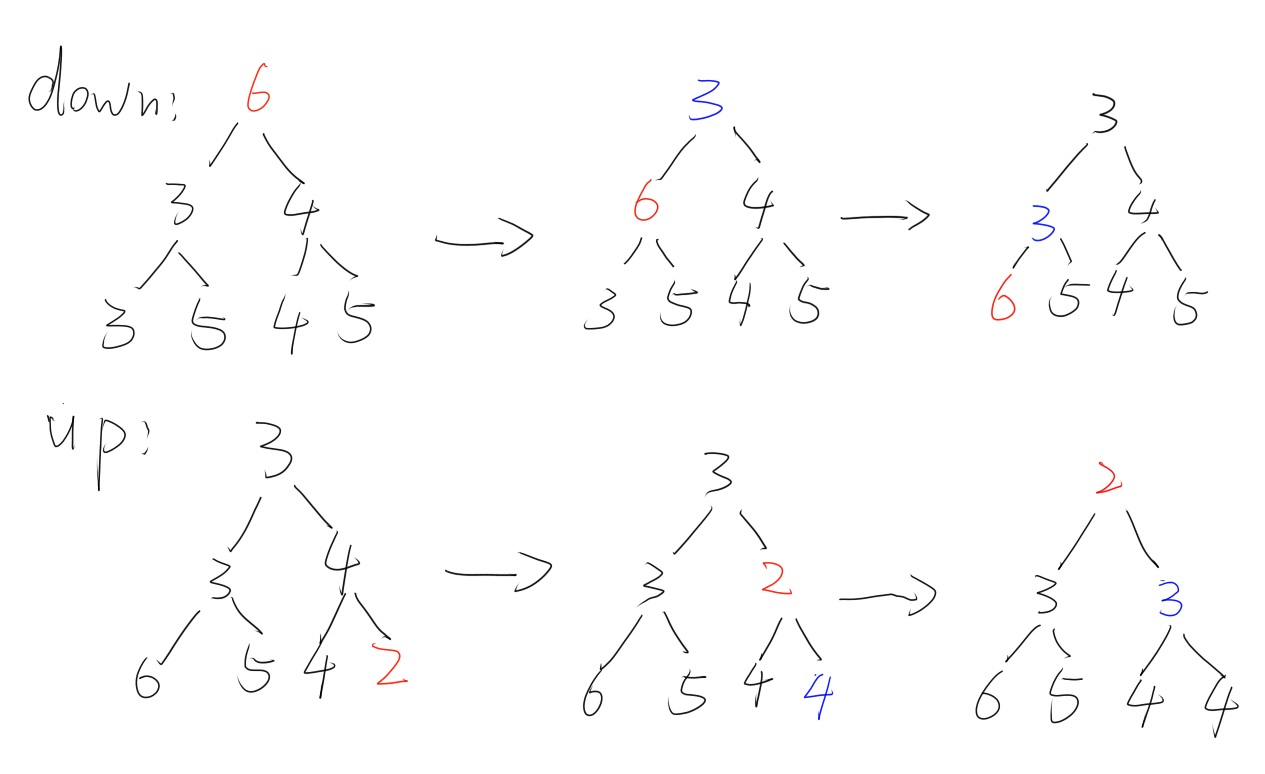
$down(x)$:将$x$号节点的值下移直至二叉树满足堆的性质
- 若两个子节点都比当前节点大或当前节点为叶子节点,则操作停止
- 否则,将当前节点与两个子节点的较小值进行交换,重复上一步骤
$down(x)$:将$x$号节点的值下移直至二叉树满足堆的性质
- 若父节点比当前节点大或当前节点为根节点,则操作停止
- 否则,将当前节点与父节点的值进行交换,重复上一步骤

$insert(x)$:插入一个数$x$
- 新建一个节点,其值为插入的数
heap[++size]=x;
- 将新插入的数上移
up(size);
$top()$:查找最小值:return heap[1];
$pop()$:删除最小值
- 将最小值和最后一个值交换
swap(heap[1],heap[size]),然后删除最后一个值size--;,将此时的新根节点下移down(1);
以下三个操作需要额外定义$ph,hp$数组,其中$ph[i]$表示第$i$个插入的数在堆中的下标,$hp[i]$表示堆中的第$i$号点是第几个插入的点,,交换时需交换所有数组,插入时也需记录次序。
$heap_swap(x,y)$:交换两个点
$del(k)$:删除第$k$个插入的数
- 将当前数和最后一个值交换
heap_swap(heap[k],heap[size]),然后删除最后一个值size--;,将此时的新的点下移且上移(不确定大小,都做一遍,只会执行一个)down(k);up(k);
$change(k,x)$:把第$k$个插入的数改为$x$
- 先修改
heap[k]=x,然后将新点移动down(k);up(k);
代码实现:
普通版(不包含特定点的修改删除)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| #include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,m;
int treap[N],cnt;
void up(int x){
if(x==1)return;
if(treap[x>>1]>treap[x]){
swap(treap[x],treap[x>>1]);
up(x>>1);
}
}
void down(int x){
int t=x;
if((x<<1)<=cnt&&treap[x<<1]<treap[t])t=x*2;
if((x<<1|1)<=cnt&&treap[x<<1|1]<treap[t])t=x*2+1;
if(x!=t){
swap(treap[x],treap[t]);
down(t);
}
}
void insert(int x){
treap[++cnt]=x;
up(cnt);
}
void pop(){
swap(treap[1],treap[cnt]);
cnt--;
down(1);
}
int top(){
return treap[1];
}
bool empty(){
return !cnt;
}
int size(){
return cnt;
}
int main(){
cin >> n >> m;
for(int i=1;i<=n;i++){
int tmp;
cin >> tmp;
insert(tmp);
}
for(int i=1;i<=m;i++){
cout << top() << ' ';
pop();
}
return 0;
}
|
进阶版(包含特定点操作,应用场景:$Dijkstra$):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
| #include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n;
int heap[N],cnt,alls;
int ph[N],hp[N];
void heap_swap(int x,int y){
swap(ph[hp[x]],ph[hp[y]]);
swap(hp[x],hp[y]);
swap(heap[x],heap[y]);
}
void up(int x){
if(x==1)return;
if(heap[x>>1]>heap[x]){
heap_swap(x,x>>1);
up(x>>1);
}
}
void down(int x){
int t=x;
if((x<<1)<=cnt&&heap[x<<1]<heap[t])t=x*2;
if((x<<1|1)<=cnt&&heap[x<<1|1]<heap[t])t=x*2+1;
if(x!=t){
heap_swap(x,t);
down(t);
}
}
void insert(int x,int k){
heap[++cnt]=x;
ph[k]=cnt;
hp[cnt]=k;
up(cnt);
}
void pop(){
heap_swap(1,cnt);
cnt--;
down(1);
}
int top(){
return heap[1];
}
bool empty(){
return !cnt;
}
int size(){
return cnt;
}
void del(int k){
k=ph[k];
heap_swap(k,cnt);
cnt--;
up(k);down(k);
}
void change(int k,int x){
k=ph[k];
heap[k]=x;
up(k);down(k);
}
int main(){
cin >> n;
for(int i=1;i<=n;i++){
char op[3];
cin >> op;
if(op[0]=='I'){
int x;
cin >> x;
insert(x,++alls);
}
else if(op[0]=='P'){
cout << top() << endl;
}
else if(op[0]=='C'){
int k,x;
cin >> k >> x;
change(k,x);
}
else if(op[1]=='M'){
pop();
}
else{
int k;
cin >> k;
del(k);
}
}
return 0;
}
|