平衡树
BST(Binary Search Tree):二叉搜索树
满足:
- 当前节点的左子树中的任何一个点的权值$<$当前节点的权值
- 当前节点的右子树中的任何一个点的权值$>$当前节点的权值
一般保证无重复权值,若有,可以在每个节点上记录当前权值的个数
可以发现,BST的中序遍历是有序的,因此BST的作用就是动态维护有序集合
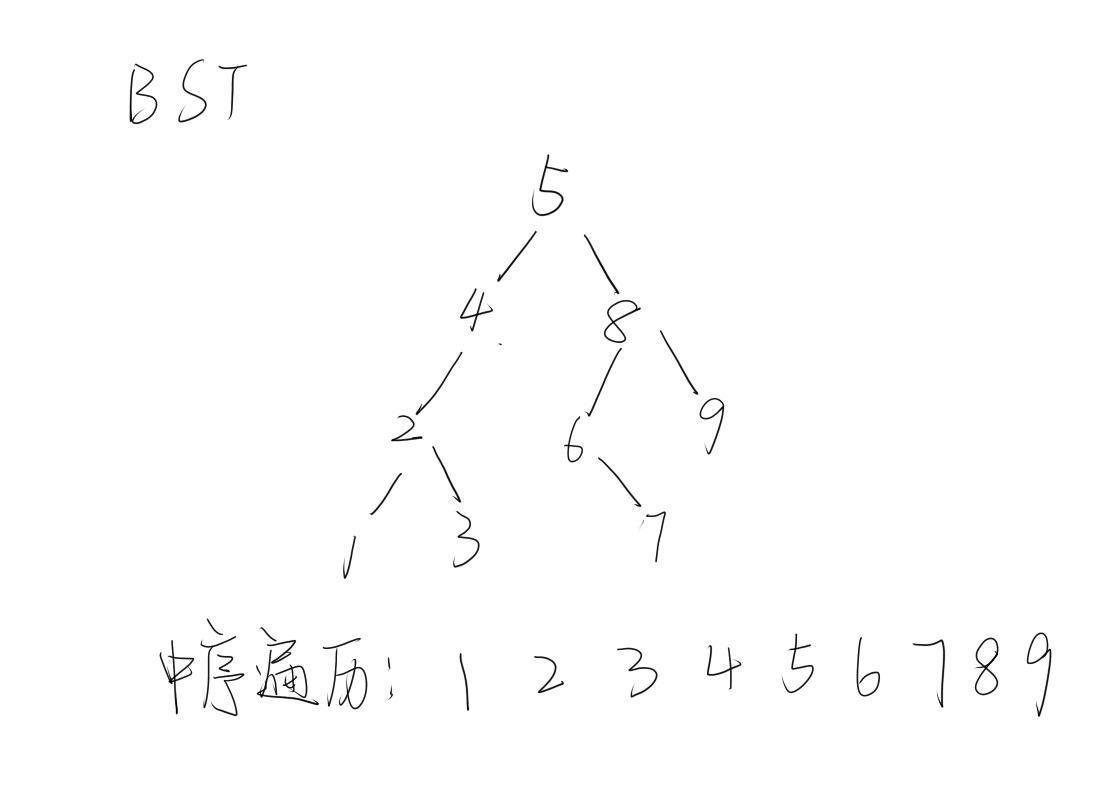
操作:
- 插入
- 删除
- 找前驱(中序遍历中的前一个位置)和后继(中序遍历中的后一个位置)
- 找最大和最小

平衡树就是特殊的二叉搜索树
普通平衡树(Treap)
Treap——Tree+heap
使用堆的性质优化二叉搜索树,使用左旋和右旋让二叉搜索树保持堆的性质使二叉树的层数尽量小,减少每次操作的复杂度。
结点的保存:
1 | struct Node{ |
初始化:新建两个哨兵结点,初始值为$-\infin,+\infin$
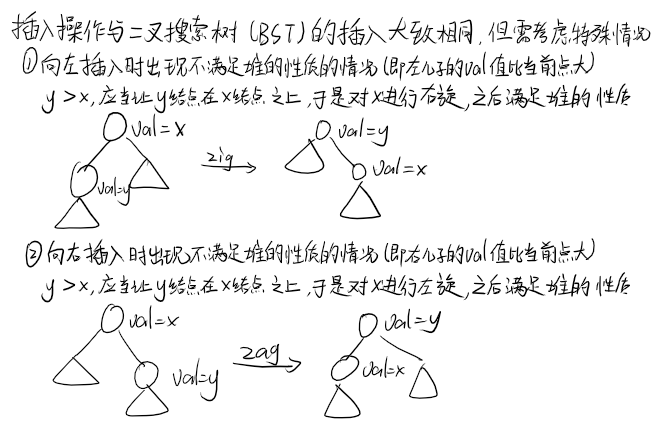
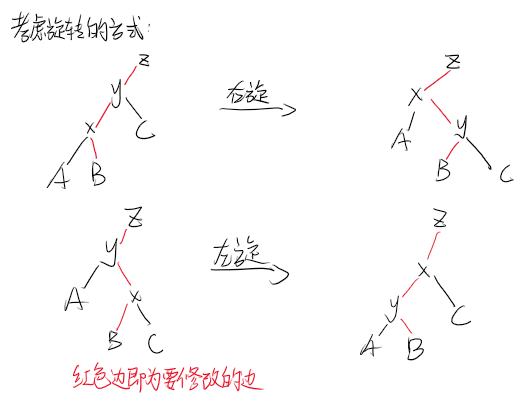
核心操作:旋转:左旋(zag),右旋(zig)
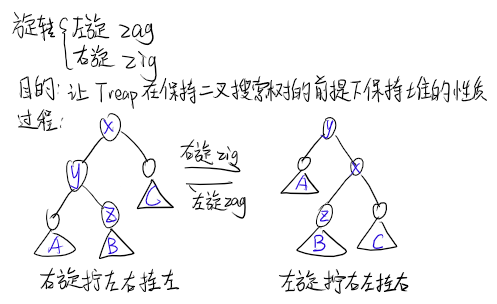
操作:
新建节点
1
2
3
4
5
6int get_node(int key){
tr[++idx].key=key;
tr[idx].val=rand();
tr[idx].cnt=tr[idx].size=1;
return idx;
}pushup(计算size)
1
2
3void pushup(int p){
tr[p].size=tr[tr[p].l].size+tr[tr[p].r].size+tr[p].cnt;
}左旋右旋
1
2
3
4
5
6
7
8
9
10
11void zig(int &p){//一定要传引用,此时p代表指向根节点的指针(根会改变)
int q=tr[p].l;
tr[p].l=tr[q].r,tr[q].r=p,p=q;//右挂左,拧左,改变指向根节点的指针
pushup(tr[p].r),pushup(p);
}
void zag(int &p){
int q=tr[p].r;
tr[p].r=tr[q].l,tr[q].l=p,p=q;
pushup(tr[p].l),pushup(p);
}初始化(新建哨兵结点)
1
2
3
4
5
6void build(){
get_node(-INF),get_node(INF);
root=1,tr[1].r=2;
pushup(root);
if (tr[1].val<tr[2].val)zag(root);//可能一开始就不符合堆的性质,旋转
}插入:与二叉搜索树的插入相同,但是插入完后需要旋转保持堆的性质

1
2
3
4
5
6
7
8
9
10
11
12
13void insert(int &p,int key){//更新结点时也要更新祖先节点的相应值,所以也要传引用
if(!p)p=get_node(key);
else if(tr[p].key==key)tr[p].cnt++;
else if(tr[p].key>key){
insert(tr[p].l,key);
if(tr[tr[p].l].val>tr[p].val)zig(p);
}
else{
insert(tr[p].r,key);
if(tr[tr[p].r].val>tr[p].val)zag(p);
}
pushup(p);
}删除

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25void remove(int &p,int key){
if(!p)return;
if(tr[p].key==key){
if(tr[p].cnt>1)tr[p].cnt--;
else if(tr[p].l||tr[p].r){
if(!tr[p].r||tr[tr[p].l].val>tr[tr[p].r].val){
zig(p);
remove(tr[p].r,key);
}
else{
zag(p);
remove(tr[p].l,key);
}
}
else p=0;
}
else if(tr[p].key>key){
remove(tr[p].l,key);
}
else{
remove(tr[p].r,key);
}
pushup(p);
}通过数值找排名
注意:因为有哨兵结点的存在,最终求的排名比实际多一位

1
2
3
4
5
6
7
8
9
10
11
12int get_rank_by_key(int p,int key){
if(!p)return 0;//找不到
if(tr[p].key==key)return tr[tr[p].l].size+1;
if(tr[p].key>key)return get_rank_by_key(tr[p].l,key);
return tr[tr[p].l].size+tr[p].cnt+get_rank_by_key(tr[p].r,key);
}
int main(){
...
get_rank_by_key(root,key)-1;
...
}通过排名找数值
注意:因为有哨兵结点的存在,查找时应查的排名应加一

1
2
3
4
5
6
7
8
9
10
11
12int get_key_by_rank(int p,int rank){
if(!p)return INF;
if(tr[tr[p].l].size>=rank)return get_key_by_rank(tr[p].l,rank);
if(tr[tr[p].l].size+tr[p].cnt>=rank)return tr[p].key;
return get_key_by_rank(tr[p].r,rank-tr[tr[p].l].size-tr[p].cnt);
}
int main(){
...
get_key_by_rank(root,rank+1);
...
}找前驱(严格小于k的最大数)

1
2
3
4
5int get_prev(int p,int key){
if(!p)return -INF;
if(tr[p].key>=key)return get_prev(tr[p].l,key);
return max(tr[p].key,get_prev(tr[p].r,key));
}找后继(严格大于k的最小数)
与找前驱类似
1
2
3
4
5int get_next(int p,int key){
if(!p)return INF;
if(tr[p].key<=key)return get_next(tr[p].r,key);
return min(tr[p].key,get_next(tr[p].l,key));
}
总模板:
1 |
|
文艺平衡树(Splay)
支持序列中区间翻转的平衡二叉树,保证中序遍历为当前序列的顺序
存储:
1 | struct Node{ |
核心:每操作一个结点(插入,查询),都将该结点旋转到树根
维护信息(size,懒标记flag(记录翻转)):
pushup:维护信息(当前点的size等于左右儿子的size之和加1)
旋转之后
pushdown:下传懒标记(翻转左右子树后标记下传)
递归之前
核心操作:
旋转rotate(x)

1
2
3
4
5
6
7
8
9
10
11void rotate(int x){
int y=tr[x].p,z=tr[y].p;
int k=tr[y].s[1]==x;//k=0表示x是y的左儿子;k=1表示x是y的右儿子
tr[z].s[tr[z].s[1]==y]=x,tr[x].p=z;
//改变y和z,x和z的关系,z的y原先所在儿子变为x,x的父节点变为z
tr[y].s[k]=tr[x].s[k^1],tr[tr[x].s[k^1]].p=y;
//改变y和x的相反儿子的关系,y的x原先所在儿子变为x的相反儿子,x的原先相反儿子的父节点变为y
tr[x].s[k^1]=y,tr[y].p=x;
//改变x和y的关系,x的相反儿子变为y,y的父节点变为x
pushup(y),pushup(x);
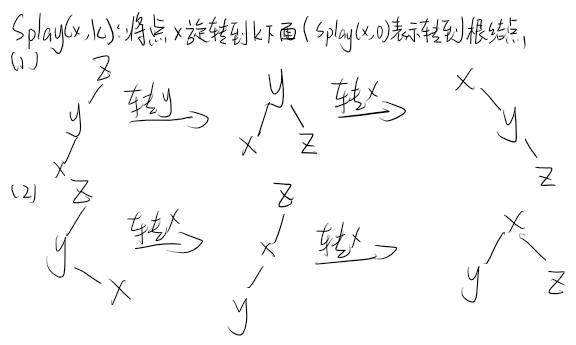
}splay(x,k):

1
2
3
4
5
6
7
8
9
10
11void splay(int x,int k){
while(tr[x].p!=k){
int y=tr[x].p,z=tr[y].p;
if(z!=k){
if((tr[y].s[1]==x)^(tr[z].s[1]==y)) rotate(x);
else rotate(y);
}
rotate(x);
}
if(!k)root=x;
}插入

1
2
3
4
5
6
7
8void insert(int v){
int u=root,p=0;
while(u)p=u,u=tr[u].s[v>tr[u].v];
u=++idx;
if(p)tr[p].s[v>tr[p].v]=u;
tr[u].init(v,p);
splay(u,0);
}删除

通过排名找数值
1
2
3
4
5
6
7
8
9
10int get_k(int k){
int u=root;
while(true){
pushdown(u);
if(tr[tr[u].s[0]].size>=k)u=tr[u].s[0];
else if(tr[tr[u].s[0]].size+1==k)return u;
else k-=tr[tr[u].s[0]].size+1,u=tr[u].s[1];
}
return -1;
}输出序列(中序遍历)
1
2
3
4
5
6void output(int u){
pushdown(u);
if(tr[u].s[0])output(tr[u].s[0]);
if(tr[u].v>=1&&tr[u].v<=n)cout << tr[u].v << ' ';
if(tr[u].s[1])output(tr[u].s[1]);
}
其余操作参考Treap
总模板:
1 |
|
FHQ-Treap
1 |
|