并查集

操作：

1. 将两个集合合并
2. 询问两个元素是否在一个集合中

暴力算法：合并$O(n)$，查询$O(1)$

并查集：

基本原理：每个集合用一棵树来表示，树根的编号就是整个集合的编号。每个节点用$fa$数组存储父节点

问题1：如何判断树根:fa[x]==x

问题2：如何查找树根:while(fa[x]!=x)x=fa[x]

问题3：如何合并两个集合:求出$x,y$两点所在树的根节点$fa_x,fa_y$，把其中一个根节点连到另一棵树的根节点上fa[x]=y

这样就实现了并查集的基本操作，但可以发现此时的复杂度依然可以达到$O(n)$,于是考虑优化

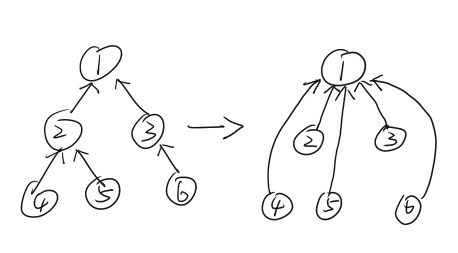
路径压缩优化：查找树根时更新父节点直到根节点

按秩合并：把深度较小的树连接到深度较大的树的根节点上，例：

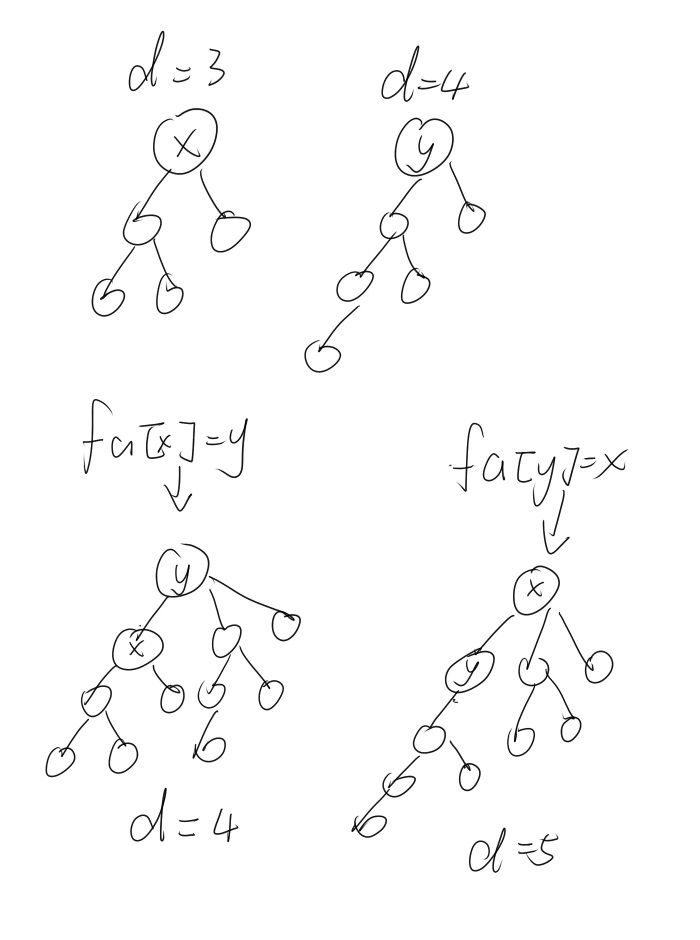
可以发现，把深度较小的树连接到深度较大的树上，合并后的树的深度小，因为查询的复杂度与深度正相关，所以这样的复杂度较低。

可以使用$d$数组维护每个节点所在树的深度，实际实现中只需记录根节点的深度即可。

优化后复杂度近似为$O(1)$

定义及初始化：

1
2
3
4

int fa[N],d[N],sz[N];//d,sz为深度和大小，是维护的额外信息
for(int i=1;i<=n;i++){
    fa[i]=i,d[i]=1,sz[i]=1;
}

查找(路径压缩)：

1
2
3

int find(int x){
    return fa[x]==x?x:fa[x]=find(fa[x]);
}

合并（按秩合并）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

void merge(int x,int y){
    x=find(x),y=find(y);
    if(x==y)return;
    if(d[x]>d[y]){
        fa[y]=x;
        sz[x]+=sz[y];
    }
    else if(d[x]<d[y]){
        fa[x]=y;
        sz[y]+=sz[x];
    }
    else{
        fa[x]=y;
        d[y]++;
        sz[y]+=sz[x];
    }
}

一般不使用按秩合并：

1
2
3
4
5
6

void merge(int x,int y){
    x=find(x),y=find(y);
    if(x==y)return;
    fa[x]=y;
    sz[y]+=sz[x];
}

带权并查集

例题：P2024 NOI2001 食物链

用每一个点到根节点的距离表示这个点与根节点的关系

$\left {\begin{matrix} dis \equiv 1 (\bmod 3) & 当前点被根吃\ dis \equiv 2 (\bmod 3) & 根被当前点吃 \ dis \equiv 0 (\bmod 3) & 当前点与根同类\end{matrix}\right.$