快速傅里叶变换（FFT）

快速傅里叶变换用于解决多项式乘法（卷积）问题

给定一个 $ n $ 次多项式 $ F(x) = a_0 + a_1x + a_2x^2+…+a_nx^n $。

以及一个 $ m $ 次多项式 $ G(x) = b_0 + b_1x + b_2x^2+…+b_mx^m $。

已知 $ H(x) = F(x) \cdot G(x) = c_0 + c_1x + c_2x^2+…+c_{n+m}x^{n+m} $。

请你计算并输出 $ c_0,c_1,…,c_{n+m} $。

FFT 可以将朴素的 $O(n^2)$ 算法优化为 $O(n\log n)$

前置知识

多项式

有一个 $n$ 次多项式 $A(x)=a_0+a_1x+\cdots +a_n x^n$

性质：用任 $n+1$ 个不同点均可确定一个 $n$ 次多项式（点表示法）

证明：任取 $n+1$ 个不同数 $x_0 \sim x_n$，代入 $A(x)$ 得到 $y_0\sim y_n$，则可以得到方程组：
$$
\left{\begin{matrix}
a_0+a_1x_0+\cdots +a_nx_0^n=y_0\
a_0+a_1x_1+\cdots +a_nx_1^n=y_1\
\cdots \
a_0+a_1x_n+\cdots +a_nx_n^n=y_n
\end{matrix}\right.
$$
由于 $x_0 \sim x_n,y_0 \sim y_n$ 均为已知，因此这个方程组就是一个 $n+1$ 元一次方程组

该方程组的系数行列式（$n+1$ 阶范德蒙行列式）
$$
\begin{bmatrix}
1& x_0& x_0^2&\cdots & x_0^n \
1& x_1& x_1^2&\cdots & x_1^n \
\vdots & \vdots & \vdots & \ddots & \vdots \
1& x_n& x_n^2&\cdots & x_n^n
\end{bmatrix}
=\prod _{1\le i < j \le n+1}(x_i-x_j) \ne 0
$$
则由克莱姆法则，该线性方程组有唯一解

复数

设复数 $z=a+bi$

称 $x$ 轴为实轴， $y$ 轴为虚轴，则这样的平面称为复平面。 $z$ 在复平面对应的点为 $Z(a,b)$，向量 $\overrightarrow{OZ}$ 与实轴正方向的夹角称为 $z$ 的辐角，记作 $\text{Arg } z$，满足 $\text{Arg } z\in (-\pi,\pi]$ 的辐角叫作 $z$ 的辐角主值，记作 $\arg z$

复数乘法的几何意义：设 $z=z_1 \cdot z_2$，则 $|\vec{z}|=|\vec {z_1}|+|\vec{z_2}|,\arg z=\arg z_1+\arg z_2$

在复平面上取单位圆，将单位圆等分成 $n$ 份，第 $k$ 份对应的复数记作 $\omega_n^k$，$|\omega_n^k|=1,\arg \omega_n^k =k\frac {2\pi} n$，则 $\omega_n^k$ 称作 $n$ 次单位根

性质：

$\omega_n^i \ne \omega_n^j,\forall i \ne j$
$\omega_n^k=\cos \frac {2k\pi} n +i\sin\frac{2k\pi} n$
$\omega_n^0=\omega_n^n=1$
$\omega_{2n}^{2k}=\omega_n^k$
$\omega_n^{k+\frac n 2}=-\omega_n^k$

快速傅里叶变换

将多项式转化为点

设 $A(x)=a_0+a_1x+\cdots +a_{n-1}x^{n-1}$
$$
\begin{array}{l}
A(x)\
=a_0+a_1x+\cdots +a_{n-1}x^{n-1}\
=(a_0+a_2x^2+\cdots +a_{n-2}x^{n-2})+(a_1x+a_3x^3+\cdots +a_{n-1}x^{n-1})\
=(a_0+a_2x^2+\cdots +a_{n-2}x^{n-2})+x(a_1+a_3x^2+\cdots +a_{n-1}x^{n-2})
\end{array}
$$
记 $A_1(x)=a_0+a_2x+\cdots +a_{n-2}x^{\frac n 2-1},A_2(x)=a_1+a_3x+\cdots +a_{n-1}x^{\frac n 2-1}$

则 $A(x)=A_1(x^2)+xA_2(x^2)$

取 $n$ 次单位根 $\omega_n^0 \sim \omega_n^{n-1}$ 代入 $A(x)$

若 $k\in [0,\frac n 2 -1]$，
$$
\begin{array}{l}
A(\omega_n^k)\
=A_1(\omega_n^{2k})+\omega_n^kA_2(\omega_n^{2k})\=A_1(\omega_{\frac n 2}^{k})+\omega_n^kA_2(\omega_{\frac n 2}^{k})
\end{array}
$$

若 $k \in [\frac n 2,n-1]$，相当于 $k \in [0, \frac n 2 -1]$ ，$k’=k+\frac n 2$
$$
\begin{array}{l}
A(\omega_n^{k+\frac n 2})\
=A_1(\omega_n^{2k+n})+\omega_n^{k+\frac n 2}A_2(\omega_n^{2k+n})\
=A_1(\omega_n^{2k})+\omega_n^{k+\frac n 2}A_2(\omega_n^{2k})\
=A_1(\omega_{\frac n 2}^{k})-\omega_n^{k}A_2(\omega_{\frac n 2}^{k})
\end{array}
$$
可以发现，若要求 $A(\omega_n^k)$，则只需求两个长度为 $\frac n 2$ 的序列 $A_1(\omega_{\frac n 2}^k),A_2(\omega_{\frac n 2}^k)$，它们各自也可以按照这种方式划分为两个部分，由此产生蝶形算法

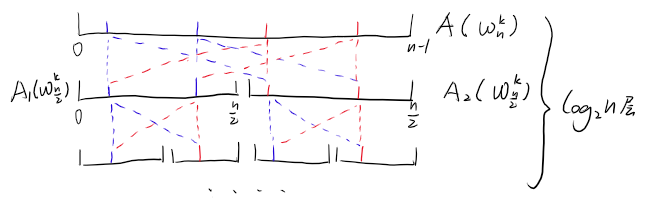
时间复杂度 $O(n \log n)$

快速傅里叶逆变换

将点还原为多项式

设 $A(x)=a_0+a_1x+\cdots +a_{n-1}x^{n-1}$

已知 $n$ 个点 $(\omega_n^k,A(\omega_n^k))$，记 $A(\omega_n^k)=y_k$，令 $c_k=\sum_{i=0}^{n-1} y_i(w_n^{-k})^i$，则 $c_k=na_k$

则令 $B(x)=y_0+y_1x+\cdots+y_{n-1}x^{n-1}$，那么 $c_k=B(\omega _n^{-k})$

也就是求 $B(\omega_n^0) \sim B(\omega_n^{-(n-1)})$，等价于求 $$B(\omega_n^n) \sim B(\omega_n^{1})$$，因此可以用快速傅里叶变换求出

下面证明 $c_k=na_k$
$$
\begin{array}{l}
c_k\
=\sum_{i=0}^{n-1} y_i(w_n^{-k})^i\
=\sum_{i=0}^{n-1} (\sum_{j=0}^{n-1} a_j(\omega_n^i)^j)(\omega_n^{-k})^i\
=\sum_{i=0}^{n-1} (\sum_{j=0}^{n-1} a_j(\omega_n^j)^i)(\omega_n^{-k})^i\
=\sum_{i=0}^{n-1} (\sum_{j=0}^{n-1} a_j(\omega_n^{j-k})^i)\
=\sum_{j=0}^{n-1} (\sum_{i=0}^{n-1} a_j(\omega_n^{j-k})^i)\
=\sum_{j=0}^{n-1} a_j(\sum_{i=0}^{n-1} (\omega_n^{j-k})^i)
\end{array}
$$
令 $S(x)=1+x+x^2+\cdots+x^{n-1}$

若 $k \ne 0$，则
$$
\begin{array}{l}
S(\omega_n^k)=1+\omega_n^k+\omega_n^{2k}+\cdots+\omega_n^{(n-1)k}\
\omega_n^k S(\omega_n^k)=\omega_n^k+\omega_n^{2k}+\cdots+\omega_n^{(n-1)k}+\omega_n^{nk}=1+\omega_n^k+\omega_n^{2k}+\cdots+\omega_n^{(n-1)k}=S(\omega_n^k)\
\therefore (\omega_n^k-1) S(\omega_n^k)=0\
\because k \ne 0\
\therefore \omega_n^k \ne 1\
\therefore S(\omega_n^k)=0
\end{array}
$$
若 $k=0$，则 $\omega_n^0=1,S(1)=n$

因此
$$
\begin{array}{l}
c_k\
=\sum_{j=0}^{n-1} a_j(\sum_{i=0}^{n-1} (\omega_n^{j-k})^i)\
=\sum_{j=0}^{n-1} a_j(S(\omega_n^{j-k}))\
=na_k
\end{array}
$$

蝶形算法

以 $n=8$ 为例：

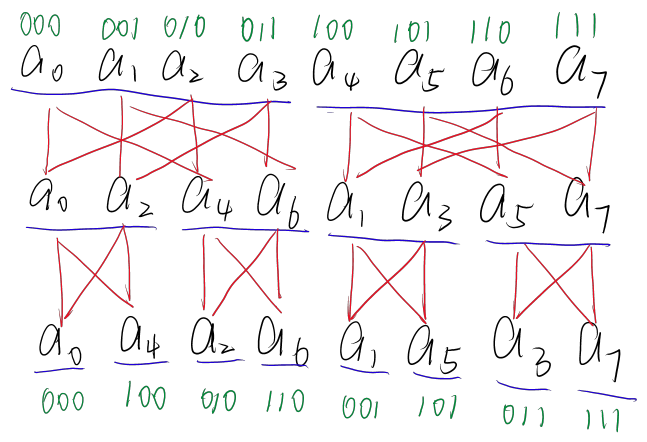
则需要先预处理下面一行的顺序，写出上下每个数的二进制表示，不难看出下面一行每个数的二进制就是上面一行对应数二进制表示翻转形成的

记下面一行第 $i$ 个数的编号为 $(rev[i]=rev[i\gg1]\gg1)|((rev[i])&1 \ll (bit-1))$，其中 $bit$ 表示位数，即将当前数的最低位取出，将剩余位右移，然后把取出的数放到最高位。

至此，算法结束。

洛谷 P3803 【模板】多项式乘法（FFT）/AcWing 3122. 多项式乘法

#include<bits/stdc++.h>
using namespace std;

const int N=3e5+5;
const double PI=acos(-1);
int n,m;
struct Complex{//复数
    double x,y;
    Complex operator+(const Complex &t)const{
        return {x+t.x,y+t.y};
    }
    Complex operator-(const Complex &t)const{
        return {x-t.x,y-t.y};
    }
    Complex operator*(const Complex &t)const{
        return {x*t.x-y*t.y,x*t.y+y*t.x};
    }
}a[N],b[N];
int rev[N],bit,tot;

void fft(Complex a[],int inv){
    for(int i=0;i<tot;i++){//调整顺序
        if(i<rev[i]){
            swap(a[i],a[rev[i]]);
        }
    }
    for(int mid=1;mid<tot;mid<<=1){//从倒数第二层开始向上计算，mid是每一段长度的一半
        auto w1=Complex({cos(PI/mid),inv*sin(PI/mid)});//w_n^1，方便后面运算，若inv=1，表示正变换，即从w0~wn-1，否则为逆变换，即从wn~w1
        for(int i=0;i<tot;i+=mid*2){//一段一段枚举
            auto wk=Complex({1,0});//当前段的单位根
            for(int j=0;j<mid;j++,wk=wk*w1){//
                auto x=a[i+j],y=wk*a[i+j+mid];//x=A1(wk),y=A2(wk)
                a[i+j]=x+y,a[i+j+mid]=x-y;//A(wk)=A1(wk)+wk*A2(wk),A(wk+mid)=A1(wk)-wk*A2(wk)
            }
        }
    }
}

int main(){
    cin >> n >> m;
    for(int i=0;i<=n;i++)cin >> a[i].x;
    for(int i=0;i<=m;i++)cin >> b[i].x;
    while((1<<bit)<n+m+1)bit++;//这里要将tot定为最小的满足tot>=n+m+1的数，2^bit=tot
    tot=1<<bit;
    for(int i=0;i<tot;i++){//求出最后一行的顺序
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
    }
    fft(a,1),fft(b,1);//正变换
    for(int i=0;i<tot;i++){
        a[i]=a[i]*b[i];
    }
    fft(a,-1);//逆变换
    for(int i=0;i<=n+m;i++){
        cout << (int)(a[i].x/tot+0.5) << ' ';//防止出现0.999->0,加上0.5
    }
    return 0;
}

例题：洛谷 P1919 【模板】高精度乘法 | A*B Problem 升级版/AcWing 3123. 高精度乘法II

给定两个正整数 $ A $ 和 $ B $，请你计算 $ A \times B $ 的值。

输入格式
共两行，第一行包含整数 $ A $，第二行包含整数 $ B $。

输出格式
共一行，包含 $ A \times B $ 的值。

数据范围
$ 1 \le A与B的长度 \le 10^5 $。

输入样例：
1
2
2
3
输出样例：
1
6

分析：

设 $A=\overline {a_{n-1}a_{n-2}\cdots a_1a_0}$

则 $A=a_{n-1}10^{n-1}+a_{n-2}10^{n-2}+\cdots + a_0+10^0$

设 $A(x)=a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\cdots+a_0x^0$

则 $A=A(10)$，同理 $B=B(10)$

则 $C(10)=A(10)B(10)$，使用 FFT 优化即可。

#include<bits/stdc++.h>
using namespace std;

const int N=3e6+5;
const double PI=acos(-1);
int n,m;
char s1[N],s2[N];
int res[N];
struct Complex{
    double x,y;
    Complex operator+(const Complex &t)const{
        return {x+t.x,y+t.y};
    }
    Complex operator-(const Complex &t)const{
        return {x-t.x,y-t.y};
    }
    Complex operator*(const Complex &t)const{
        return {x*t.x-y*t.y,x*t.y+y*t.x};
    }
}a[N],b[N];
int rev[N],bit,tot;

void fft(Complex a[],int inv){
    for(int i=0;i<tot;i++){
        if(i<rev[i]){
            swap(a[i],a[rev[i]]);
        }
    }
    for(int mid=1;mid<tot;mid<<=1){
        auto w1=Complex({cos(PI/mid),inv*sin(PI/mid)});
        for(int i=0;i<tot;i+=mid*2){
            auto wk=Complex({1,0});
            for(int j=0;j<mid;j++,wk=wk*w1){
                auto x=a[i+j],y=wk*a[i+j+mid];
                a[i+j]=x+y,a[i+j+mid]=x-y;
            }
        }
    }
}

int main(){
    cin >> s1 >> s2;
    n=strlen(s1)-1,m=strlen(s2)-1;
    for(int i=0;i<=n;i++)a[i].x=s1[n-i]-'0';
    for(int i=0;i<=m;i++)b[i].x=s2[m-i]-'0';
    while((1<<bit)<n+m+1)bit++;
    tot=1<<bit;
    for(int i=0;i<tot;i++){
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
    }
    fft(a,1),fft(b,1);
    for(int i=0;i<tot;i++){
        a[i]=a[i]*b[i];
    }
    fft(a,-1);
    
    //处理进位
    int k=0;
    for(int i=0,t=0;i<tot||t;i++){
        t+=a[i].x/tot+0.5;
        res[k++]=t%10;
        t/=10;
    }
    
    while(k>1&&!res[k-1])k--;
    for(int i=k-1;i>=0;i--)cout << res[i] ;
    return 0;
}

本文采用署名-非商业性使用-相同方式共享 4.0 国际许可协议，转载请注明出处。