搜索
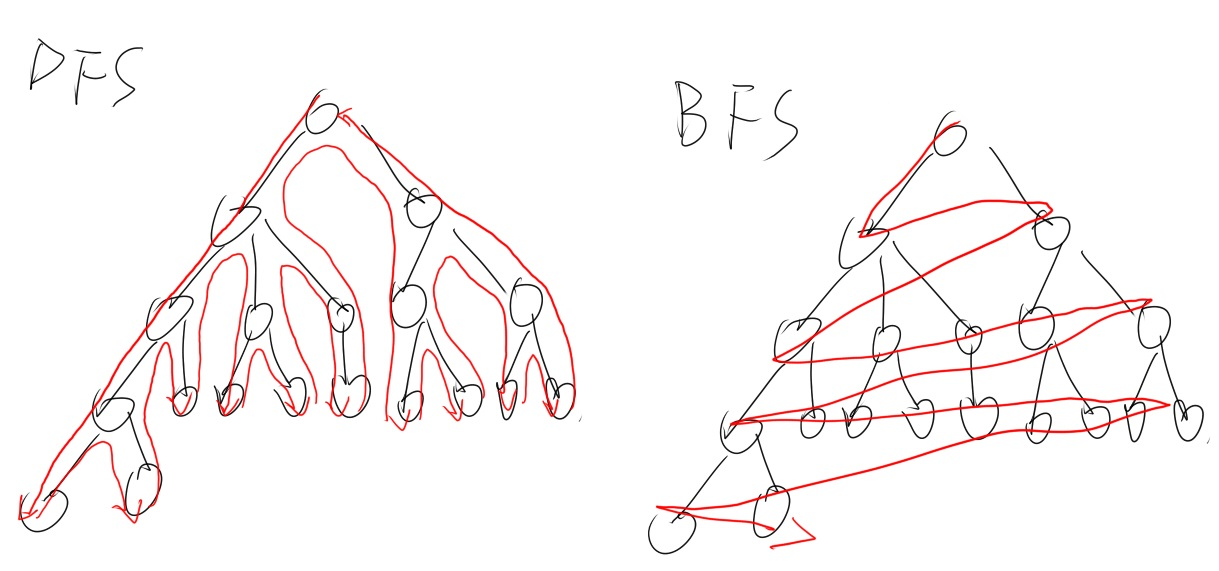
深度优先搜索($DFS$),广度优先搜索($BFS$)

对比:
|
数据结构 |
空间 |
|
| $DFS$ |
$stack$ |
$O(h)$ |
不具最短性 |
| $BFS$ |
$queue$ |
$O(2^h)$ |
最短路 |
$DFS$:
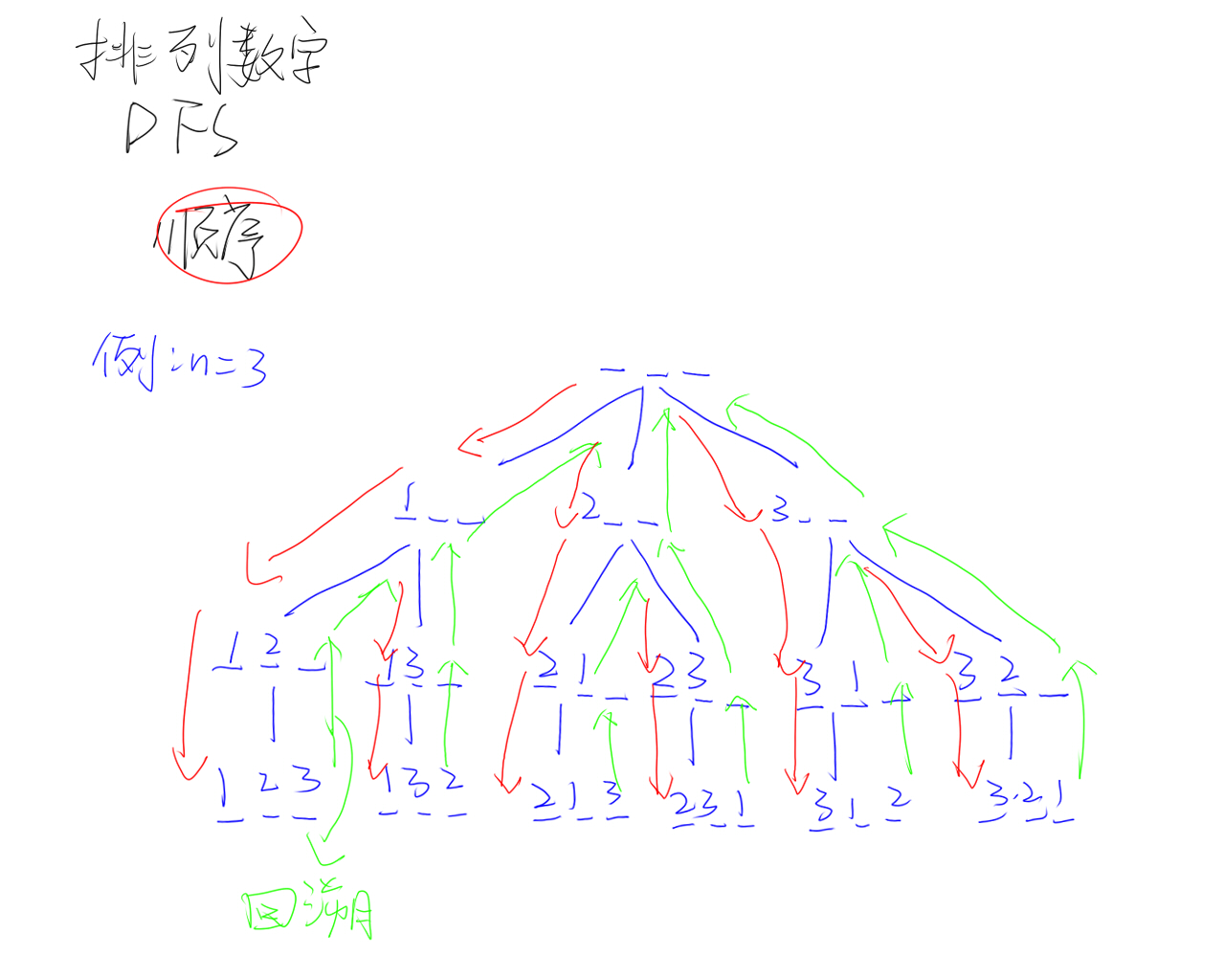
例1:给定一个数字$n$,输出$1\sim n$的全排列(按字典序)
考虑顺序与回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| #include<bits/stdc++.h>
using namespace std;
const int N=10;
int n;
int num[N];
bool use[N];
void dfs(int now){
if(now>n){
for(int i=1;i<=n;i++){
cout << num[i] << ' ';
}
cout << endl;
return;
}
for(int i=1;i<=n;i++){
if(!use[i]){
use[i]=1;
num[now]=i;
dfs(now+1);
use[i]=0;
}
}
}
int main(){
cin >> n;
dfs(1);
return 0;
}
|
例2:n皇后问题
给定一个整数$n$,表示在$n*n$的棋盘上摆放$n$个皇后,保证每行,每列,每一斜线只有一个皇后,求所有的摆放方法
分析:类似上一题,每次摆放时判断当前点是否可以放,若放,标记行、列、斜线,进入下一行
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| #include<bits/stdc++.h>
using namespace std;
const int N=20;
int n;
char g[N][N];
bool col[N],dg[N],udg[N];
void dfs(int u){
if(u==n){
for(int i=0;i<n;i++){
cout << g[i] << endl;
}
cout << endl;
}
for(int i=0;i<n;i++){
if(!col[i]&&!dg[u+i]&&!udg[n-u+i]){
g[u][i]='Q';
col[i]=dg[u+i]=udg[n-u+i]=true;
dfs(u+1);
col[i]=dg[u+i]=udg[n-u+i]=false;
g[u][i]='.';
}
}
}
int main(){
cin >> n;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
g[i][j]='.';
}
}
dfs(0);
return 0;
}
|
$BFS$:
每次扩展队列中的元素,若扩展后的点符合要求即入队,搜索到终点后或队列为空停止
例2:给定一个$n*m$的迷宫,其中$0$表示路,$1$表示墙,求从左上走到右下的最短长度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| #include<bits/stdc++.h>
using namespace std;
const int N=105;
int n,m;
int mp[N][N];
int d[N][N];
int dx[5]={0,0,0,-1,1},dy[5]={0,1,-1,0,0};
void bfs(){
memset(d,-1,sizeof d);
d[1][1]=0;
queue<pair<int,int>>q;
q.push({1,1});
while(!q.empty()){
auto t=q.front();
q.pop();
int x=t.first,y=t.second;
if(x==n&&y==m){
cout << d[x][y] << endl;
break;
}
for(int i=1;i<=4;i++){
if(x+dx[i]>n||x+dx[i]<1||y+dy[i]>m||y+dy[i]<1)continue;
if(mp[x+dx[i]][y+dy[i]])continue;
if(d[x+dx[i]][y+dy[i]]==-1){
d[x+dx[i]][y+dy[i]]=d[x][y]+1;
q.push({x+dx[i],y+dy[i]});
}
}
}
}
int main(){
cin >> n >> m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin >> mp[i][j];
}
}
bfs();
return 0;
}
|