数据结构

目录

树状数组

$lowbit(x)$：$x$二进制下第一个1

1
2
3
int lowbit(x){
    return x&-x;
}

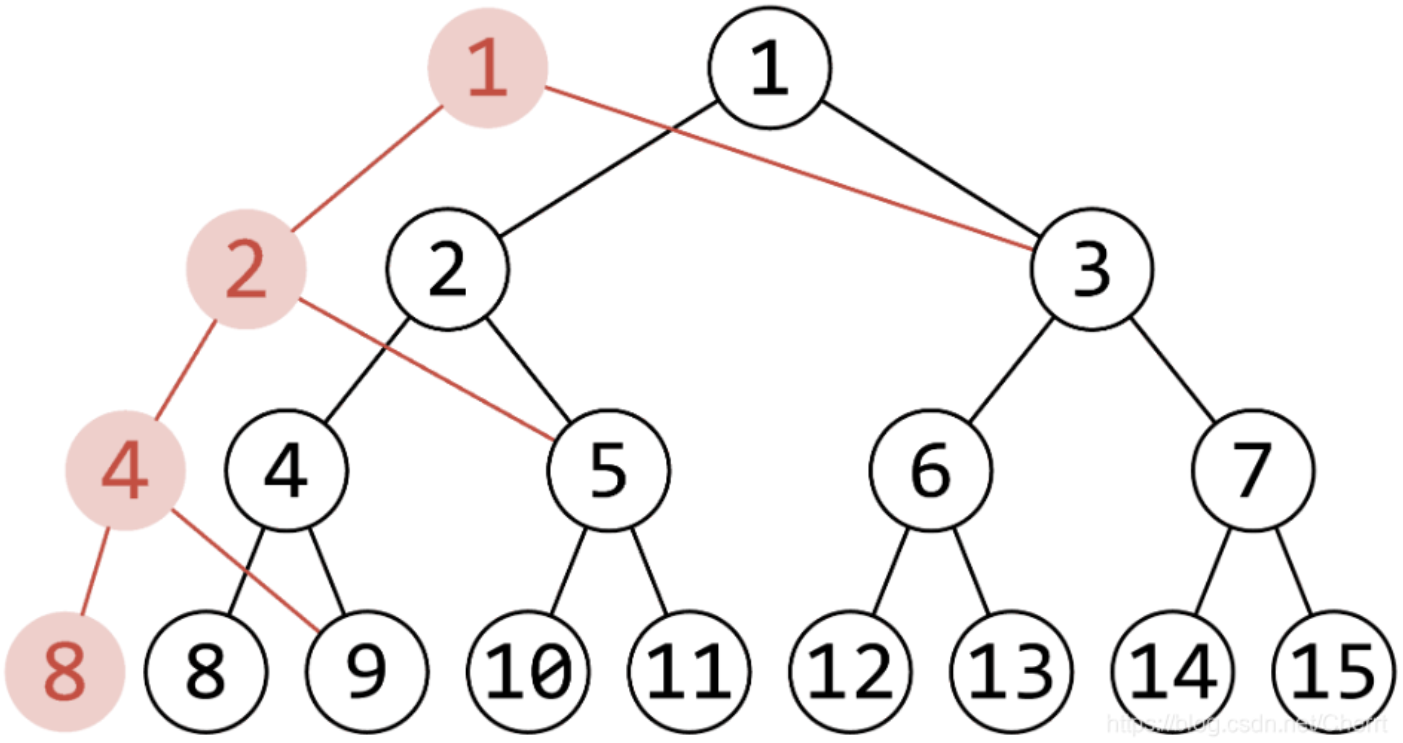
支配区间：$[i-lowbit(i)+1,i]$

引理1：对于任意x,y，其支配区间要么相离，要么呈包含与被包含关系

这说明，支配区间的关系构成一棵树，这棵树就是树状数组

引理2：对于点x，其在树上的父节点为$x+lowbit(x)$

由此可以得到单点修改和前缀查询的方法

单点修改：假设我们将$a_x$增加了$k$，考虑其对${c_n}$的影响。注意到，所有支配区间包含$x$的点，对应一条从$x$到根的链，于是，我们不断将$c_x$加上$k$，并令$x=x+lowbit(x)$即可。

前缀查询：令$S(r)=\sum_{i=1}^{r}a_i$，则有
$$
S(r)=S(r-lowbit(r))+\sum_{i=r-lowbit(r)+1}^{r}a_i
$$
因此，$S(r)=S(r-lowbit(r))+b_r$。我们不断将答案加上$b_r$，并令$r=r-lowbit(r)$，直到$r=0$即可。

对于区间查询，其可拆为两个前缀和相减的形式。

线性建树：先将所有 $c_i$ 赋值为 $a_i$，再枚举 $i = 1, 2, · · · , n$，若 $i + lowbit(i) \le n$， 将 $c_{i+lowbit(i)}$ 加上 $c_i$ 即可。

1
2
3
4
5
for(int i=1;i<=n;i++){
	c[i]+=a[i];
    int j=i+lowbit(i);
    if(j<=n)c[j]+=c[i];
}

模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <bits/stdc++.h>
using namespace std;
const int N=500010;
int n,m;
int a[N];
long long tr[N];

int lowbit(int x){
    return x&-x;
}
void add(int x,int c){
    for(int i=x;i<=n;i+=lowbit(i)){
        tr[i]+=c;
    }
}
long long sum(int x){
    long long res=0;
    for(int i=x;i;i-=lowbit(i)){
        res+=tr[i];
    }
    return res;
}
int main()
{
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        cin >> a[i];
    }
    for(int i=1;i<=n;i++){
        tr[i]+=a[i];
        int j=i+lowbit(i);
        if(j<=n)tr[j]+=tr[i];
    }
    while(m--){
        int op;
        int l,d,r;
        cin >> op >> l;
        if(op==1){
            cin >> d;
            add(l,d);
        }
        else{
            cin >> r;
            cout << sum(r)-sum(l-1) << endl;
        }
    }
    return 0;
}

例题1：洛谷P6225 [eJOI2019] 异或橙子

[eJOI2019] 异或橙子

题目描述

Janez 喜欢橙子！他制造了一个橙子扫描仪，但是这个扫描仪对于扫描的每个橙子的图像只能输出一个 $32$ 位整数。

他一共扫描了 $n$ 个橙子，但有时他也会重新扫描一个橙子，导致这个橙子的 $32$ 位整数发生更新。

Janez 想要分析这些橙子，他觉得异或操作非常有趣，他每次选取一个区间从 $l$ 至 $u$，他想要得到这个区间内所有子区间的异或和的异或和。

例如 $l=2,u=4$ 的情况，记橙子序列 $A$ 中第 $i$ 个橙子的整数是 ，那么他要求的就是：

$$a_2 \oplus a_3 \oplus a_4 \oplus (a_2\oplus a_3)\oplus(a_3\oplus a_4)\oplus(a_2\oplus a_3 \oplus a_4)$$

注：式子中的 $\oplus$ 代表按位异或运算。异或的运算规则如下。

对于两个数的第 $i$ 位，记为 $x,y$，那么：

$x$ $y$ $x\oplus y$
$0$ $1$ $1$
$1$ $0$ $1$
$0$ $0$ $0$
$1$ $1$ $0$

例：$13\oplus 23=26$

$13=$ $0\cdots 001101$
$23=$ $0\cdots 010111$
$13\oplus 23=$ $0\cdots 011010$

输入格式

第一行输入两个正整数 $n,q$，表示橙子数量和操作次数。

接下来一行 $n$ 个非负整数，表示每个橙子扫描得到的数值 ，从 $1$ 开始编号。

接下来 $q$ 行，每行三个数：

  • 如果第一个数是 $1$，接下来输入一个正整数 $i$ 与非负整数 $j$，表示将第 $i$ 个橙子的扫描值 $a_i$ 修改为 $j$。

  • 如果第一个数是 $2$，接下来输入两个正整数 $u,l$ 表示询问这个区间的答案。

输出格式

对于每组询问，输出一行一个非负整数，表示所求的总异或和。

样例 #1

样例输入 #1

1
2
3
4
5
3 3
1 2 3
2 1 3
1 1 3
2 1 3

样例输出 #1

1
2
2
0

样例 #2

样例输入 #2

1
2
3
4
5
6
7
8
5 6
1 2 3 4 5
2 1 3
1 1 3
2 1 5
2 4 4
1 1 1
2 4 4

样例输出 #2

1
2
3
4
2
5
4
4

提示

输入输出样例 1 解释

  • 最初，$A=[1,2,3]$，询问结果为 $1\oplus 2\oplus 3\oplus(1\oplus 2)\oplus (2\oplus 3)\oplus(1\oplus 2\oplus 3)=2$

  • 修改后，第一个位置被修改为 $3$ ，询问的结果是 $3\oplus 2\oplus 3\oplus(3\oplus 2)\oplus (2\oplus 3)\oplus(3\oplus 2\oplus 3)=0$。

数据规模与约定：

本题采用多测试点捆绑测试，共有 5 个子任务。

  • Subtask 1(12 points)：$1\le n,q\le 10^2$，无特殊限制
  • Subtask 2(18 points)：$1\le n,q\le 5\times 10^2$，且没有修改操作。
  • Subtask 3(25 points)：$1\le n,q\le 5\times 10^3$，无特殊限制
  • Subtask 4(20 points)：$1\le n,q\le 2\times 10^5$，且没有修改操作。
  • Subtask 5(25 points)：$1\le n,q\le 2\times 10^5$，无特殊限制

对于所有数据，$0\le a_i\le 10^9,1\le n,q\le 2\times 10^5$

说明

原题来自：eJOI2019 Problem A. XORanges

题面&数据来自：LibreOJ

形式化题面：

给定$n,q(1\le n,q \le 2\times 10^5)$及长度为$n$的序列${a_1,a_2,\cdots,a_n}$，支持以下两种命令

  • 单点修改
  • 查询一段区间所有子区间的异或和的异或和

分析：

性质：$x \oplus 0=x,x\oplus x =0$

通过手动模拟可以发现：当区间长度为偶数，即$l,u$奇偶性不同时，所有数的贡献都为偶数次，因此答案为$0$；当区间长度为奇数，即$l,u$奇偶性相同时，所有与$l$奇偶性相同的数的贡献为奇数次，其它数的贡献为偶数，所以答案为$a_l\oplus a_{l+2}\oplus \cdot\cdot\cdot \oplus a_u$

由于是单点修改区间的异或和查询的问题，故可以用树状数组，用两个树状数组分别存储奇数位置和偶数位置的异或值，修改和查询时分别在两个数组中查询即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include<bits/stdc++.h>
using namespace std;

const int N=2e5+5;
int n,q;
int a[N];
int tr1[N],tr2[N];

int lowbit(int x){
    return x&-x;
}

void add(int x,int c){
    if(x%2)for(int i=x;i<=n;i+=lowbit(i))tr1[i]^=c;
    else for(int i=x;i<=n;i+=lowbit(i))tr2[i]^=c;
}

int sum1(int x){
    int res=0;
    for(int i=x;i;i-=lowbit(i))res^=tr1[i];
    return res;
}

int sum2(int x){
    int res=0;
    for(int i=x;i;i-=lowbit(i))res^=tr2[i];
    return res;
}

int main(){
    cin >> n >> q;
    for(int i=1;i<=n;i++){
        cin >> a[i];
        add(i,a[i]);
    }
    for(int i=1;i<=q;i++){
        int op,x,y;
        cin >> op >> x >> y;
        if(op==1){
            add(x,a[x]^y);
            a[x]=y;
        }
        else{
            if((y-x+1)%2==0)cout << 0;
            else{
                if(x%2==1){
                    cout << (sum1(y)^sum1(x-1));
                }
                else{
                    cout << (sum2(y)^sum2(x-1));
                }
            }
            cout << endl;
        }
    }
    return 0;
}

例题2：洛谷P3372 【模板】线段树 1（树状数组实现区间操作）

【模板】线段树 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

  1. 将某区间每一个数加上 $k$。
  2. 求出某区间每一个数的和。

输入格式

第一行包含两个整数 $n, m$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $m$ 行每行包含 $3$ 或 $4$ 个整数，表示一个操作，具体如下：

  1. 1 x y k：将区间 $[x, y]$ 内每个数加上 $k$。
  2. 2 x y：输出区间 $[x, y]$ 内每个数的和。

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

样例输出 #1

1
2
3
11
8
20

提示

对于 $30%$ 的数据：$n \le 8$，$m \le 10$。
对于 $70%$ 的数据：$n \le {10}^3$，$m \le {10}^4$。
对于 $100%$ 的数据：$1 \le n, m \le {10}^5$。

保证任意时刻数列中所有元素的绝对值之和 $\le {10}^{18}$。

【样例解释】

形式化题面：

给定$n,q(1\le n,q \le 10^5)$及长度为$n$的序列，支持区间加，区间查询总和。

分析：

需要实现树状数组的区间修改，可以考虑差分。

先考虑区间加：定义树状数组$b$的每个元素$b_i=a_i-a_{i-1}$，则在$[l,r]$区间加$x$即为$b_l+x,b_{r+1}-x$。

在考虑区间查询：此时区间$[l,r]$的和为$\sum_{i=l}^r\sum_{j=1}^ib_j$，考虑每个数的贡献，可以得出：
$$
\sum_{i=l}^r\sum_{j=1}^ib_j=\sum_{j=1}^{l-1}b_j\times(r-l+1)+\sum_{j=l}^rb_j\times(r-j+1)
$$
可以发现，第一部分就是树状数组的前缀和，直接求即可，而第二部分无法直接求出，展开后可以得出：
$$
\sum_{j=l}^rb_j\times(r-j+1)=\sum_{j=l}^rb_j\times(r+1)-\sum_{j=l}^rb_j\times j
$$
可以发现，第一部分也可以直接求出，而第二部分可以新建一个树状数组$c$，令$c_i=b_i\times i$，即可求出。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include<bits/stdc++.h>
using namespace std;

const int N=1e5+5;
typedef long long ll;
int n,m;
ll a[N];
ll b[N],c[N];
ll lowbit(ll x){
    return x&-x;
}

ll sum1(ll x){
    ll sum=0;
    for(int i=x;i;i-=lowbit(i)){
        sum+=b[i];
    }
    return sum;
}

ll sum2(ll x){
    ll sum=0;
    for(int i=x;i;i-=lowbit(i)){
        sum+=c[i];
    }
    return sum;
}

void add1(ll x,ll k){
    for(int i=x;i<=n;i+=lowbit(i)){
        b[i]+=k;
    }
}

void add2(ll x,ll k){
    for(int i=x;i<=n;i+=lowbit(i)){
        c[i]+=x*k;
    }
}

int main(){
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        cin >> a[i];
    }
    for(int i=1;i<=n;i++){
        b[i]+=a[i]-a[i-1];
        int j=i+lowbit(i);
        if(j<=n)b[j]+=b[i];
    }
    for(int i=1;i<=n;i++){
        c[i]+=(a[i]-a[i-1])*i;
        int j=i+lowbit(i);
        if(j<=n)c[j]+=c[i];
    }
    for(int i=1;i<=m;i++){
        int op;
        cin >> op;
        if(op==1){
            ll l,r,x;
            cin >> l >> r >> x;
            add1(l,x),add1(r+1,-x);
            add2(l,x),add2(r+1,-x);
        }
        else{
            ll l,r;
            cin >> l >> r;
            cout << sum1(l-1)*(r-l+1)+(sum1(r)-sum1(l-1))*(r+1)-(sum2(r)-sum2(l-1)) << endl;
        }
    }
    return 0;
}

例题3：树状数组上倍增

形式化题面：

给定长度为 $n(n \le 10^5 )$ 的序列 $a$ 和$ q(q \le 10^5 ) $次命令，每次命令形如$ x, y, k$，表示将 $a_x$ 改为 $y$，并立即查询序列中第 $k$ 小的数。 保证任意时刻 $a$ 中的任意元素均不超过 $10^5$。

分析：

先考虑暴力做法，考虑二分答案，建立一个存储每个数的出现次数的树状数组，每次二分并查询前缀和，复杂度为$O(n\log^2n)$。

考虑优化，使用倍增，令$d=\lceil \log_2n\rceil,\cdots,1,0$，将初始为$0$的$ans$每次加上$2^d$，判断是否合法即可。可以发现新增的区间为$[ans+1,ans+2^d]$，而这刚好对应树状数组中第$2^d$位的值($ans$在二进制下的最低位一定为$2^d$，而树状数组每个点对应的区间，即支配区间为$[x-lowbit(x)+1,x]$，刚好就是新增的区间)，因此可以使用倍增。

注意：倍增时为了防止出现当加上当前位个数超过$k$，不加当前位个数少于$k$的情况，可以判断个数小于$k$，最后的答案加$1$即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include<bits/stdc++.h>
using namespace std;

const int N=1e5+5;
int n,q;
int inc[20];
int a[N],cnt[N],b[N];
int last[20];
int lowbit(int x){
    return x&-x;
}

void change(int x,int k){
    for(int i=a[x];i<N;i+=lowbit(i)){
        b[i]--;
    }
    for(int i=k;i<N;i+=lowbit(i)){
        b[i]++;
    }
    a[x]=k;
}

int main(){
    for(int i=0,j=1;i<=17;i++){
        inc[i]=j;
        j<<=1;
    }
    cin >> n >> q;
    for(int i=1;i<=n;i++){
        cin >> a[i];
        cnt[a[i]]++; 
    }
    for(int i=1;i<N;i++){
        b[i]+=cnt[i];
        int j=i+lowbit(i);
        if(j<N)b[j]+=b[i];
    }
    for(int i=1;i<=q;i++){
        int x,y,k;
        cin >> x >> y >> k;
        change(x,y);
        int cnt=0,ans=0;
        for(int j=17;j>=0;j--){
            ans+=1<<j;
            if(ans>=N||cnt+b[ans]>=k)ans-=1<<j;
            else cnt+=b[ans];
        }
        cout << ans+1 << endl;
    }
    return 0;
}

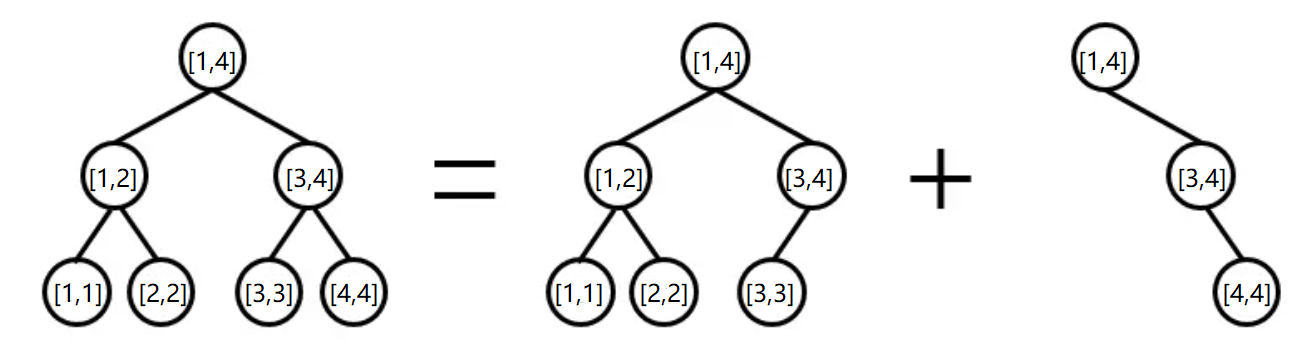
线段树

线段树是一种分治型结构，每个结点维护一个区间的信息。线段树的根为$[1,n]$。对于每个节点$[l,r]$，令$mid=\lfloor\frac{l+r}{2}\rfloor$，则其左儿子为$[l,m]$，右儿子为$[m+1,r]$。

线段树的基础操作包括单点修改查询，区间修改（懒标记），区间查询。

模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e6+5;
typedef long long ll;
ll a[maxn],w[maxn*4];
void pushup(const int u){
    w[u]=w[u*2]+w[u*2+1];
}
//建立线段树
void build(const int u,int L,int R){
    if(L==R){
        w[u]=a[L];
        return;
    }
    int M=(L+R)/2;
    build((u*2),L,M);
    build((u*2)+1,M+1,R);
    pushup(u);
}
//懒标记
ll lzy[maxn*4];
void maketag(int u,int len,ll x){
    lzy[u]+=x;
    w[u]+=len*x;
}
void pushdown(int u,int L,int R){
    int M=(L+R)/2;
    maketag(u*2,M-L+1,lzy[u]);
    maketag(u*2+1,R-M,lzy[u]);
    lzy[u]=0;
}
//单点查询修改
ll query1(int u,int L,int R,int p){
    pushdown(u,L,R);
    if(L==R){
        return w[u];
    }
    else {
        int M=(L+R)/2;
        if(M>=p)
            return query1((u*2),L,M,p);
        else
            return query1((u*2)+1,M+1,R,p);
    }
    return 0;
}
void update1(int u,int L,int R,int p,ll x){
    if(L==R){
        w[u]=x;
    }
    else{
        int M=(L+R)/2;
        if(M>=p)
            update1((u*2),L,M,p,x);
        else
            update1((u*2)+1,M+1,R,p,x);
        pushup(u);
    }
}


//区间查询
bool InRange(int L,int R,int l,int r){
    return (l<=L)&&(R<=r);
}

bool OutofRange(int L,int R,int l,int r){
    return (L>r)||(R<l);
}
ll query(int u,int L,int R,int l,int r){
    if(InRange(L,R,l,r)){
        return w[u];
    }
    if(OutofRange(L,R,l,r))
        return 0;
    else{
        int M=(L+R)/2;
        pushdown(u,L,R);
        return query((u*2),L,M,l,r)+query((u*2)+1,M+1,R,l,r);
    }
    return 0;
}
//修改
void update(int u,int L,int R,int l,int r,ll x){
    if(InRange(L,R,l,r)){
        maketag(u,R-L+1,x);
    }
    else if(!OutofRange(L,R,l,r)){
        int M=(L+R)/2;
        pushdown(u,L,R);
        update((u*2),L,M,l,r,x);
        update((u*2)+1,M+1,R,l,r,x);
        pushup(u);
    }
}
int main()
{
    ios::sync_with_stdio(false);
    int n,m;
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        cin >> a[i];//输入每一项的值
    }
    build(1,1,n);//建立线段树
    for(int t=1;t<=m;t++){
        int op,x,y;
        ll k;
        cin >> op;
        if(op==1){
            cin >> x >> y >> k;
            update(1,1,n,x,y,k);//修改，x到y加k
        }
        else{
            cin >> x >> y;
            cout << query(1,1,n,x,y) << endl;//查询x到y
        }
    }
    return 0;
}

线段树的使用条件：

  • 对于一个操作含区间修改，区间查询的问题，什么时候可以使用线段树？

    1. 对于一次区间修改，若要对某个节点打上标记，能够快速更新该节点的信息(update & pushdown)
    2. 标记在知晓前后顺序时能够合并(pushdown)
    3. 对于所有无标记的节点，能够根据两个子节点的信息，推出当前节点的信息(pushup)

    综上，可以实现update，pushdown，pushup就可以使用线段树

线段树标记永久化：

  • 什么时候可以不下传标记？

    • 有些时候是可以的，例如：

      区间加，区间查询和问题。对于一次查询，设目前查询区间为$[l,r]$，查询区间为$[L,R]$，设该点处的懒标记为$ v$，则能产生$[l,r],[L,R]$交的长度$\times v$的贡献，额外加上即可。

    • 有些时候并不可以的，例如：

      区间赋值，区间查询和问题。

      维护若干个等长向量，每次将一段区间发向量乘上某个矩阵、区间查询向量和问题。

    综上，线段树能够实现标记永久化，必须满足懒标记的合并具有交换律，即懒标记合并的结果与它们的先后顺序无关。

例题1：洛谷P3401改编（线段树维护复杂信息）

形式化题面：

给定$n,q(1 \le n,q \le 10^5)$及长度为$n$的序列，支持单点修改，查询一个区间的所有子区间的异或和的总和。保证序列中的每个元素$\le 1023$

分析：

可以考虑拆位维护。

对于二进制下的第$d$位，建立一个线段树维护区间的异或和为$1$的子区间个数，最后将答案加上个数乘上$2^d$即可。

考虑如何维护节点信息，即通过两个子节点得到当前节点的异或和为$1$的子区间个数，可以发现这个值就是左右儿子自己的异或和为$1$的子区间个数与跨越中点的异或和为$1$的子区间个数之和，因此可以在每个点上维护$p0,p1,q0,q1$，分别表示前缀异或和为$0,1$，后缀异或和为$0,1$的个数，设一个节点的左右儿子为$L,R$，则这个节点的跨越中点的异或和为$1$的子区间个数为$q0(L)\times p1(R)+q1(L)\times p0(R)$。

考虑如何维护$p0,p1,q0,q1$。

  • 若左子区间的异或和为$0$，则$p0=p0(L)+p0(R),p1=p1(L)+p1(R)$
  • 若左子区间的异或和为$1$，则$p0=p0(L)+p1(R),p1=p1(L)+p0(R)$
  • 若右子区间的异或和为$0$，则$q0=q0(R)+q0(L),q1=q1(R)+q1(L)$
  • 若右子区间的异或和为$1$，则$q0=q0(R)+q1(L),q1=q1(R)+q0(L)$

因此还需维护$sum$，表示区间的异或和。

考虑如何查询，可以重载$+$号，当区间合并时按照上面的步骤计算出新的区间即可。

总的时间复杂度为$O(n\log^2n)$

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
const ll N=1e5+5;
struct node{
    ll cnt;
    bool sum;
    ll p0,p1,q0,q1;
    ll len;
    friend node operator+(node a,node b){
		node c;
    	if(a.len==0&&b.len)return b;
        if(a.len&&b.len==0)return a;
        if(a.len==0&&b.len==0)return c;
        c.len=a.len+b.len;
        c.sum=a.sum^b.sum;
        c.cnt=a.cnt+b.cnt+a.q0*b.p1+a.q1*b.p0;
        if(a.sum==0){
            c.p0=a.p0+b.p0;
            c.p1=a.p1+b.p1;
        }
        else{
            c.p0=a.p0+b.p1;
            c.p1=a.p1+b.p0;
        }
        if(b.sum==0){
            c.q0=b.q0+a.q0;
            c.q1=b.q1+a.q1;
        }
        else{
            c.q0=b.q0+a.q1;
            c.q1=b.q1+a.q0;
        }
        return c;
    }
}tr[12][4*N],empty;
ll n,q;

void init(int k,int u,int l,int r){
	if(l>r)return;
	tr[k][u].len=r-l+1;
	if(l<r){
		int mid=l+r>>1;
		init(k,u<<1,l,mid);
		init(k,u<<1|1,mid+1,r);
	}
}

void pushup(ll k,ll u){
    tr[k][u]=tr[k][u<<1]+tr[k][u<<1|1];
}

void change(ll k,ll to,ll u,ll l,ll r,ll x){
    if(l==r){
        node &t=tr[k][u];
        t.sum=x;
        if(x){
            t.cnt=1;
            t.p0=0;
            t.p1=1;
            t.q0=0;
            t.q1=1;
        }
        else{
            t.cnt=0;
            t.p0=1;
            t.p1=0;
            t.q0=1;
            t.q1=0;
        }
        return;
    }
    ll mid=l+r>>1;
    if(to<=mid)change(k,to,u<<1,l,mid,x);
    else change(k,to,u<<1|1,mid+1,r,x);
    pushup(k,u);
}

void modify(ll x,ll k){
    ll wei=0;    
    while(k){
        ll t=k%2;
        change(wei,x,1,1,n,t);
        k>>=1;	
        wei++;
    }
    for(int i=wei;i<10;i++){
    	change(i,x,1,1,n,0);//清空高位
    }
}

node query(ll k,ll u,ll l,ll r,ll L,ll R){
	if(R<l||L>r){
        return empty;
    }
    if(L<=l&&R>=r){
        return tr[k][u];
    }
    ll mid=l+r>>1;
    return query(k,u<<1,l,mid,L,R)+query(k,u<<1|1,mid+1,r,L,R);
}

ll find(ll l,ll r){
    ll res=0;
    for(ll i=0;i<=10;i++){
        node t=query(i,1,1,n,l,r);
        res+=t.cnt*(1<<i);
    }
    return res;
}

int main(){
    cin >> n >> q;
	for(int i=0;i<=10;i++){
    	init(i,1,1,n);
    }
    for(ll i=1;i<=n;i++){
        ll x;
        cin >> x;
        modify(i,x);
    }
    for(ll i=1;i<=q;i++){
        ll op,a,b;
        cin >> op >> a >> b;
        if(op==1){
            modify(a,b);
        }
        else{
            cout << find(a,b) << endl;
        }
    }
    return 0;
}

例题2：洛谷P4198 楼房重建（线段树维护前缀最值）

楼房重建

题目描述

小 A 的楼房外有一大片施工工地，工地上有 $N$ 栋待建的楼房。每天，这片工地上的房子拆了又建、建了又拆。他经常无聊地看着窗外发呆，数自己能够看到多少栋房子。

为了简化问题，我们考虑这些事件发生在一个二维平面上。小 A 在平面上 $(0,0)$ 点的位置，第 $i$ 栋楼房可以用一条连接 $(i,0)$ 和 $(i,H_i)$ 的线段表示，其中 $H_i$ 为第 $i$ 栋楼房的高度。如果这栋楼房上任何一个高度大于 $0$ 的点与 $(0,0)$ 的连线没有与之前的线段相交，那么这栋楼房就被认为是可见的。

施工队的建造总共进行了 $M$ 天。初始时，所有楼房都还没有开始建造，它们的高度均为 $0$。在第 $i$ 天，建筑队将会将横坐标为 $X_i$ 的房屋的高度变为 $Y_i$（高度可以比原来大—修建，也可以比原来小—拆除，甚至可以保持不变—建筑队这天什么事也没做）。请你帮小 A 数数每天在建筑队完工之后，他能看到多少栋楼房？

输入格式

第一行两个正整数 $N,M$。

接下来 $M$ 行，每行两个正整数 $X_i,Y_i$。

输出格式

$M$ 行，第 $i$ 行一个整数表示第 $i$ 天过后小 A 能看到的楼房有多少栋。

样例 #1

样例输入 #1

1
2
3
4
5
3 4
2 4
3 6
1 1000000000
1 1

样例输出 #1

1
2
3
4
1
1
1
2

提示

对于 $100%$ 的数据，$1 \le X_i \le N$，$1 \le Y_i \le 10^9$，$1\le N,M \le 10^5$。

分析：

使用线段树维护区间内可以被看见的楼房数，考虑如何维护信息。

用线段树记录每个点的斜率，若这个点前面的所有点的斜率均小于这个点的斜率，则当前楼房可以被看见。

设左儿子为$L$，右儿子为$R$，右儿子的左右儿子为$R_L,R_R$，下面分情况考虑：

  • 当$L$的最大值$M$大于等于$R_L$的最大值$m$时，$R_L$产生不了任何贡献，递归求$R_R$的贡献即可。
  • 当$L$的最大值$M$小于$R_L$的最大值$m$时，$L$对于$R_R$产生不了影响，而$R_R$的贡献在计算$R$时已经求出，因此只需递归求$R_L$的贡献即可。

因此需维护可以被看见的楼房数$cnt$，区间最大值$max$和右子区间的贡献$conribution$即可。

记$solve(R,M)$为右儿子的贡献，则当$M\ge m$时，$solve(R,M)=solve(R_R,M)$，当$M<m$时，$solve(R,M)=solve(R_L,M)+contribution_{R_R}$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include<bits/stdc++.h>
using namespace std;

const int N=4e5+5;
int n,m;
double tr_max[N];
int len[N];
double a[N];
int solve(int u,int l,int r,double maxh){
    if(l==r){
        if(a[l]>maxh)return 1;
        return 0;
    }
    if(tr_max[u]<=maxh)return 0;
    if(a[l]>maxh)return len[u];
    int mid=l+r>>1;
    if(tr_max[u<<1]<=maxh)return solve(u<<1|1,mid+1,r,maxh);
    return solve(u<<1,l,mid,maxh)+len[u]-len[u<<1];
}

void pushup(int u){
    tr_max[u]=max((double)tr_max[u<<1],(double)tr_max[u<<1|1]);
}


void change(int u,int l,int r,int x,int k){
    if(l==r&&l==x){
        tr_max[u]=(double)k/(double)x;
        len[u]=1;
        return;
    }
    int mid=l+r>>1;
    if(x<=mid)change(u<<1,l,mid,x,k);
    else change(u<<1|1,mid+1,r,x,k);
    pushup(u);
    len[u]=len[u<<1]+solve(u<<1|1,mid+1,r,tr_max[u<<1]);
}

int main(){
    cin >> n >> m;
    for(int i=1;i<=m;i++){
        int x,y;
        cin >> x >> y;
        a[x]=(double)y/(double)x;
        change(1,1,n,x,y);
        cout << len[1] << endl;
    }
    return 0;
}

例题3：洛谷P7453（线段树维护矩阵）

[THUSCH2017] 大魔法师

题目描述

大魔法师小 L 制作了 $n$ 个魔力水晶球，每个水晶球有水、火、土三个属性的能量值。小 L 把这 $n$ 个水晶球在地上从前向后排成一行，然后开始今天的魔法表演。

我们用 $A_i,B_i,C_i$ 分别表示从前向后第 $i$ 个水晶球（下标从 $1$ 开始）的水、火、土的能量值。

小 L 计划施展 $m$ 次魔法。每次，他会选择一个区间 $[l,r]$，然后施展以下 $3$ 大类、$7$ 种魔法之一：

  1. 魔力激发：令区间里每个水晶球中特定属性的能量爆发，从而使另一个特定属性的能量增强。具体来说，有以下三种可能的表现形式：

    • 火元素激发水元素能量：令 $A_i=A_i+B_i$。
    • 土元素激发火元素能量：令 $B_i=B_i+C_i$。
    • 水元素激发土元素能量：令 $C_i=C_i+A_i$。

    需要注意的是，增强一种属性的能量并不会改变另一种属性的能量，例如 $A_i=A_i+B_i$ 并不会使 $B_i$ 增加或减少。

  2. 魔力增强：小 L 挥舞法杖，消耗自身 $v$ 点法力值，来改变区间里每个水晶球的特定属性的能量。具体来说，有以下三种可能的表现形式：

    • 火元素能量定值增强：令 $A_i=A_i+v$。
    • 水元素能量翻倍增强：令 $B_i=B_i\times v$。
    • 土元素能量吸收融合：令 $C_i=v$。

  3. 魔力释放：小 L 将区间里所有水晶球的能量聚集在一起，融合成一个新的水晶球，然后送给场外观众。生成的水晶球每种属性的能量值等于区间内所有水晶球对应能量值的代数和。需要注意的是，魔力释放的过程不会真正改变区间内水晶球的能量。

值得一提的是，小 L 制造和融合的水晶球的原材料都是定制版的 OI 工厂水晶，所以这些水晶球有一个能量阈值 $998244353$。当水晶球中某种属性的能量值大于等于这个阈值时，能量值会自动对阈值取模，从而避免水晶球爆炸。

小 W 为小 L（唯一的）观众，围观了整个表演，并且收到了小 L 在表演中融合的每个水晶球。小 W 想知道，这些水晶球蕴涵的三种属性的能量值分别是多少。

输入格式

从标准输入读入数据。

我们将上述的 $7$ 种魔法，从上到下依次标号为 $1\sim7$。

输入的第一行包含一个整数 $n$（$1\le n\le 2.5\times 10^5$），表示水晶球个数。

接下来 $n$ 行，每行空格隔开的 $3$ 个整数，其中第 $i$ 行的三个数依次表示 $A_i,B_i,C_i$。

接下来一行包含一个整数 $m$（$1\le m\le2.5\times 10^5$），表示施展魔法的次数。

接下来 $m$ 行，每行 $3$ 或 $4$ 个数，格式为 opt l r (v)。其中 opt 表示魔法的编号，$l,r$ 表示施展魔法的区间（保证有 $l\le r$）。特别地，如果施展 $4\sim6$ 号魔法（魔力增强），则还有一个整数 $v$，表示小 L 消耗的法力值。

输出格式

输出到标准输出。

对每个 $7$ 号魔法（魔力释放），输出一行、空格隔开的 $3$ 个整数 a b c，分别表示此次融合得到的水晶球的水、火、土元素能量值。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
2
2 3 3
6 6 6
4
7 1 2
1 1 2
4 1 2 3
7 1 2

样例输出 #1

1
2
8 9 9
23 9 9

提示

$100%$ 的数据，$n,m\le2.5\times 10^5,0\le A_i,B_i,C_i,v<998244353$

  1. $10%$ 的数据，$n\times m\le10^7$。
  2. 另外 $10%$ 的数据，每次魔法的区间均为 $[1,n]$。
  3. 另外 $10%$ 的数据，每次非询问魔法的影响区间均为 $[1,n]$，所有修改在询问之前。
  4. 另外 $10%$ 的数据，$\operatorname{opt}\in{4,5,6,7}$。
  5. 另外 $15%$ 的数据，$\operatorname{opt}\in{1,2,7}$。
  6. 另外 $15%$ 的数据，$\operatorname{opt}\in{1,2,3,5,7}$。
  7. 另外 $15%$ 的数据，$n,m\le 10^5$。
  8. 其他数据，无特殊约定。

样例解释

以下展示每次施展魔法后，两个水晶球内的能量：

1
2
3
4
(2, 3, 3) (6, 6, 6)
(5, 3, 3) (12, 6, 6)
(8, 3, 3) (15, 6, 6)
(8, 3, 3) (15, 6, 6)

分析：可以把$a_i,b_i,b_i$看作一个向量$\begin{vmatrix}a_i & b_i & c_i\end{vmatrix}$，则对于第一种操作，只需乘上
$$
\begin{vmatrix}
1 & 0 & 0\
1 & 1 & 0\
0 & 0 & 1
\end{vmatrix}
,
\begin{vmatrix}
1 & 0 & 0\
0 & 1 & 0\
0 & 1 & 1
\end{vmatrix}
,
\begin{vmatrix}
1 & 0 & 1\
0 & 1 & 0\
0 & 0 & 1
\end{vmatrix}
$$
即可。而对于第二种操作，可以令把向量加上一个元素变为：$
\begin{vmatrix}
a_i & b_i & c_i & 1
\end{vmatrix}
$，则对于第二种操作，只需乘上
$$
\begin{vmatrix}
1 & 0 & 0 & 0\
0 & 1 & 0 & 0\
0 & 0 & 1 & 0\
v & 0 & 0 & 1
\end{vmatrix}
,
\begin{vmatrix}
1 & 0 & 0 & 0\
0 & v & 0 & 0\
0 & 0 & 1 & 0\
0 & 0 & 0 & 1
\end{vmatrix}
,
\begin{vmatrix}
1 & 0 & 0 & 0\
0 & 1 & 0 & 0\
0 & 0 & 0 & 0\
0 & 0 & v & 1
\end{vmatrix}
$$
即可。因此，所有的操作乘上的矩阵为
$$
\begin{vmatrix}
1 & 0 & 0 & 0\
1 & 1 & 0 & 0\
0 & 0 & 1 & 0\
0 & 0 & 0 & 1
\end{vmatrix}
,
\begin{vmatrix}
1 & 0 & 0 & 0\
0 & 1 & 0 & 0\
0 & 1 & 1 & 0\
0 & 0 & 0 & 1
\end{vmatrix}
,
\begin{vmatrix}
1 & 0 & 1 & 0\
0 & 1 & 0 & 0\
0 & 0 & 1 & 0\
0 & 0 & 0 & 1
\end{vmatrix}
,
\begin{vmatrix}
1 & 0 & 0 & 0\
0 & 1 & 0 & 0\
0 & 0 & 1 & 0\
v & 0 & 0 & 1
\end{vmatrix}
,
\begin{vmatrix}
1 & 0 & 0 & 0\
0 & v & 0 & 0\
0 & 0 & 1 & 0\
0 & 0 & 0 & 1
\end{vmatrix}
,
\begin{vmatrix}
1 & 0 & 0 & 0\
0 & 1 & 0 & 0\
0 & 0 & 0 & 0\
0 & 0 & v & 1
\end{vmatrix}
$$
其余操作与普通线段树相同，但要注意卡常。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
#include<bits/stdc++.h>
using namespace std;

const int N=250005,mod=998244353;

struct matrix{
    int sum[4][4];
    matrix(){
        for(int i=0;i<4;i++){
            for(int j=0;j<4;j++){
                sum[i][j]=0;
            }
        }
    }
    matrix(int t[4][4]){
        for(int i=0;i<4;i++){
            for(int j=0;j<4;j++){
                sum[i][j]=t[i][j];
            }
        }
    }
    inline void operator=(matrix x){
        for(int i=0;i<4;i++){
            for(int j=0;j<4;j++){
                sum[i][j]=x.sum[i][j];
            }
        }
    }
    friend matrix operator+(matrix x,matrix y){
        matrix a;
        for(int i=0;i<4;i++){
            for(int j=0;j<4;j++){
                a.sum[i][j]=x.sum[i][j]+y.sum[i][j];
                if(a.sum[i][j]>=mod)a.sum[i][j]-=mod;
            }
        }
        return a;
    }
    friend matrix operator*(matrix x,matrix y){
        matrix a;
        for(int i=0;i<4;i++){
            for(int j=0;j<4;j++){
                a.sum[i][j]=a.sum[i][j]+(1ll*x.sum[i][0]*y.sum[0][j])%mod;
                if(a.sum[i][j]>=mod)a.sum[i][j]-=mod;
                a.sum[i][j]=a.sum[i][j]+(1ll*x.sum[i][1]*y.sum[1][j])%mod;
                if(a.sum[i][j]>=mod)a.sum[i][j]-=mod;
                a.sum[i][j]=a.sum[i][j]+(1ll*x.sum[i][2]*y.sum[2][j])%mod;
                if(a.sum[i][j]>=mod)a.sum[i][j]-=mod;
                a.sum[i][j]=a.sum[i][j]+(1ll*x.sum[i][3]*y.sum[3][j])%mod;
                if(a.sum[i][j]>=mod)a.sum[i][j]-=mod;
            }
        }
        return a;
    }
    friend bool operator==(matrix x,matrix y){
        for(int i=0;i<4;i++){
            for(int j=0;j<4;j++){
                if(x.sum[i][j]!=y.sum[i][j])return 0;
            }
        }
        return 1;
    }
};

int n,m;
matrix a[N];
matrix tr[4*N];
matrix lazy[4*N];
matrix type[7];
int typed[7][4][4]={
    {
        {1,0,0,0},
        {0,1,0,0},
        {0,0,1,0},
        {0,0,0,1}
    },
    {
        {1,0,0,0},
        {1,1,0,0},
        {0,0,1,0},
        {0,0,0,1}
    },
    {
        {1,0,0,0},
        {0,1,0,0},
        {0,1,1,0},
        {0,0,0,1}
    },
    {
        {1,0,1,0},
        {0,1,0,0},
        {0,0,1,0},
        {0,0,0,1}
    },
    {
        {1,0,0,0},
        {0,1,0,0},
        {0,0,1,0},
        {-1,0,0,1}
    },
    {
        {1,0,0,0},
        {0,-1,0,0},
        {0,0,1,0},
        {0,0,0,1}
    },
    {
        {1,0,0,0},
        {0,1,0,0},
        {0,0,0,0},
        {0,0,-1,1}
    }
};

void init(){
    type[0]=matrix(typed[0]);
    type[1]=matrix(typed[1]);
    type[2]=matrix(typed[2]);
    type[3]=matrix(typed[3]);
    type[4]=matrix(typed[4]);
    type[5]=matrix(typed[5]);
    type[6]=matrix(typed[6]);
}

void pushup(int u){
    tr[u]=tr[u<<1]+tr[u<<1|1];
}

void build(int u,int l,int r){
    lazy[u]=type[0];
    if(l==r){
        tr[u]=a[l];
        return;
    }
    int mid=l+r>>1;
    build(u<<1,l,mid);
    build(u<<1|1,mid+1,r);
    pushup(u);
}

void pushdown(int u,int l,int r){
    if(lazy[u]==type[0])return;
    int mid=l+r>>1;
    lazy[u<<1]=lazy[u<<1]*lazy[u];
    lazy[u<<1|1]=lazy[u<<1|1]*lazy[u];
    tr[u<<1]=tr[u<<1]*lazy[u];
    tr[u<<1|1]=tr[u<<1|1]*lazy[u];
    lazy[u]=type[0];
}

void modify(int u,int l,int r,int L,int R,int x){
    if(l>=L&&r<=R){
        tr[u]=tr[u]*type[x];
        lazy[u]=lazy[u]*type[x];
        return;
    }
    pushdown(u,l,r);
    int mid=l+r>>1;
    if(L<=mid)modify(u<<1,l,mid,L,R,x);
    if(R>mid)modify(u<<1|1,mid+1,r,L,R,x);
    pushup(u);
}

matrix query(int u,int l,int r,int L,int R){
    if(l>=L&&r<=R){
        return tr[u];
    }
    pushdown(u,l,r); 
    int mid=l+r>>1;
    if(L<=mid&&R>mid)return query(u<<1,l,mid,L,R)+query(u<<1|1,mid+1,r,L,R);
    else if(L<=mid)return query(u<<1,l,mid,L,R);
    else if(R>mid)return query(u<<1|1,mid+1,r,L,R);
}

int main(){
    init();
    cin >> n ;
    for(int i=1;i<=n;i++){
        cin >> a[i].sum[0][0] >> a[i].sum[0][1] >> a[i].sum[0][2];
        a[i].sum[0][3]=1;
    }
    build(1,1,n);
    cin >> m;
    for(int i=1;i<=m;i++){
        int opt,l,r;
        cin >> opt >> l >> r;
        if(opt<=3){
            modify(1,1,n,l,r,opt);
        }
        else if(opt<=6){
            int v;
            cin >> v;
            type[4].sum[3][0]=v;
            type[5].sum[1][1]=v;
            type[6].sum[3][2]=v;
            modify(1,1,n,l,r,opt);
        }
        else{
            matrix ans=query(1,1,n,l,r);
            cout << ans.sum[0][0]%mod << ' ' << ans.sum[0][1]%mod << ' ' << ans.sum[0][2]%mod << endl;
        }
    }
    return 0;
}

权值线段树：

权值线段树与线段树的结构完全相同，基本操作也相同。

二者的主要区别在于：前者维护了桶相关信息，后者维护了序列区间信息。

例如，前者支持查询序列中有多少个数落在给定区间内，后者支持查询序列一段区间的和。

动态开点线段树：

有些时候，线段树维护的值域$V$很大，不能将整个结构建出。

注意到，每次修改只会涉及$O(\log V)$个位置，我们考虑只建出所有有用的点，从而保证线段树的大小不超过$O(q \log V)$。

具体来说：

  • 对于修改操作，我们仍套用普通线段树的操作；特别的，若发现当前节点为空，则新建一个点作为当前点。注意：传参时，一定要传入引用，保证新建节点的赋值正确。
  • 对于查询操作，我们仍套用普通线段树的查询；特别的，若发现当前节点为空，则立即返回。

值得注意的是，此时点$u$的左儿子不一定是$2u$，右儿子也不一定是$2u+1$，而可能为任意值。

模板（单点修改，区间查询）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<bits/stdc++.h>
using namespace std;

const int N=1e5+5;
struct node{
    int l,r;
    int sum;
}tr[N];
int cnt;
void pushup(int u){
    tr[u].sum=tr[tr[u].l].sum+tr[tr[u].r].sum;
}

void change(int &u,int l,int r,int x,int k){
    if(!u)u=++cnt;
    if(l==r){
        tr[u].sum+=k;
        return;
    }
    int mid=l+r>>1;
    if(x<=mid)change(tr[u].l,l,mid,x,k);
    else change(tr[u].r,mid+1,r,x,k);
    pushup(u);
}

int query(int u,int l,int r,int L,int R){
    if(!u)return 0;
    if(R<l||L>r)return 0;
    if(l>=L&&r<=R)return tr[u].sum;
    int mid=l+r>>1;
    return query(tr[u].l,l,mid,L,R)+query(tr[u].r,mid+1,r,L,R);
}

int main(){
    
    return 0;
}

例题4：权值线段树上二分

形式化题面：

给定长度为 $n(n \le 10^5 )$ 的序列 $a$ 和$ q(q \le 10^5 ) $次命令，每次命令形如$ x, y, k$，表示将 $a_x$ 改为 $y$，并立即查询序列中第 $k$ 小的数。 保证任意时刻 $a$ 中的任意元素均不超过 $10^9$。

分析：

建立一个权值线段树记录区间数的个数，查询时从根节点开始，如果当前节点的左儿子的数的个数$\ge k$，则查找左儿子中第$k$小的数，否则查找右儿子中第$k$减去左儿子中数的个数的数，查到叶节点即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include<bits/stdc++.h>
using namespace std;

const int N=1e5+5,MAX=1e9;
struct node{
    int l,r;
    int sum;
}tr[120*N];
int cnt,root;
void pushup(int u){
    tr[u].sum=tr[tr[u].l].sum+tr[tr[u].r].sum;
}

void change(int &u,int l,int r,int x,int k){
    if(!u)u=++cnt;
    if(l==r){
        tr[u].sum+=k;
        return;
    }
    int mid=l+r>>1;
    if(x<=mid)change(tr[u].l,l,mid,x,k);
    else change(tr[u].r,mid+1,r,x,k);
    pushup(u);
}

int find(int u,int l,int r,int k){
    if(!u)return 0;
    if(l==r)return l;
    int mid=l+r>>1;
    if(tr[tr[u].l].sum>=k)return find(tr[u].l,l,mid,k);
    return find(tr[u].r,mid+1,r,k-tr[tr[u].l].sum);
}
int n,m;
int a[N];
int main(){
    root=1,cnt=1;
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        cin >> a[i];
        change(root,1,MAX,a[i],1);
    }
    for(int i=1;i<=m;i++){
        int x,y,k;
        cin >> x >> y >> k;
        change(root,1,MAX,a[x],-1);
        change(root,1,MAX,y,1);
        a[x]=y;
        cout << find(root,1,MAX,k) << endl;
    }
    return 0;
}

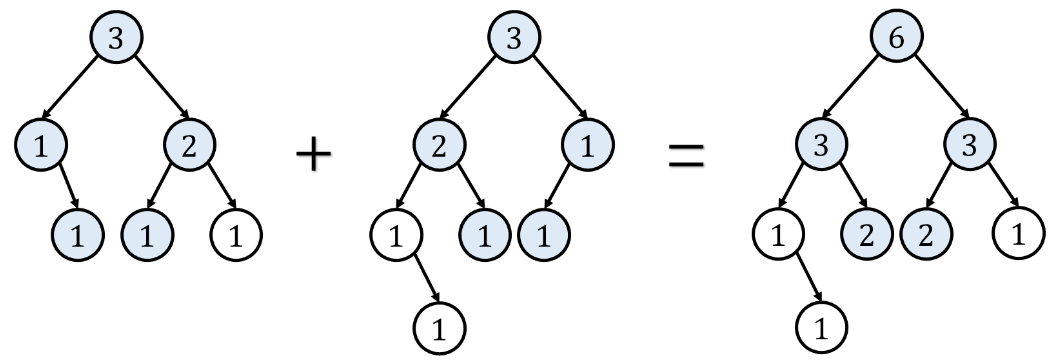
线段树合并：

权值线段树支持合并。

两个权值线段树$T_1,T_2$的合并是递归过程。具体来说，设目前要合并的两个子树分别为$T_1$中节点$x$，$T_2$中节点$y$的子树，其对应区间均为$[l,r]$，那么：

  • 首先，若$x=0$或$y=0$，则$x,y$至少一者对应一个空节点，直接返回$x+y$即可。

  • 先将$x,y$的左儿子合并，设合并后的节点编号为$p$。

  • 再将$x,y$的右儿子合并，设合并后的节点编号为$q$。

  • 将$y$的左儿子设为$p$，右儿子设为$q$，完成合并，并返回$y$表示合并后的节点编号为$y$。

  • 特别的，当$x$或$y$为叶子时，直接合并信息。

  • 注意，再合并过程中，我们需要实时下放标记$(pushdown)$，并实时更新节点信息$(pushup)$。

1
2
3
4
5
6
7
8
9
10
11
12
int merge(int x,int y,int l,int r){
    if(!x||!y)return x|y;
    if(l==r){
        tr[y].sum+=tr[x].sum;
        return y;
    }
    int mid=l+r>>1;
    tr[y].l=merge(tr[x].l,tr[y].l,l,mid)
    tr[y].r=merge(tr[x].r,tr[y].r,mid+1,r);
    pushup(y);
    return y;
}

例题5：洛谷P4556 [Vani有约会] 雨天的尾巴 /【模板】线段树合并

[Vani有约会] 雨天的尾巴 /【模板】线段树合并

题目背景

深绘里一直很讨厌雨天。

灼热的天气穿透了前半个夏天，后来一场大雨和随之而来的洪水，浇灭了一切。

虽然深绘里家乡的小村落对洪水有着顽固的抵抗力，但也倒了几座老房子，几棵老树被连根拔起，以及田地里的粮食被弄得一片狼藉。

无奈的深绘里和村民们只好等待救济粮来维生。

不过救济粮的发放方式很特别。

题目描述

首先村落里的一共有 $n$ 座房屋，并形成一个树状结构。然后救济粮分 $m$ 次发放，每次选择两个房屋 $(x, y)$，然后对于 $x$ 到 $y$ 的路径上（含 $x$ 和 $y$）每座房子里发放一袋 $z$ 类型的救济粮。

然后深绘里想知道，当所有的救济粮发放完毕后，每座房子里存放的最多的是哪种救济粮。

输入格式

输入的第一行是两个用空格隔开的正整数，分别代表房屋的个数 $n$ 和救济粮发放的次数 $m$。

第 $2$ 到 第 $n$ 行，每行有两个用空格隔开的整数 $a, b$，代表存在一条连接房屋 $a$ 和 $b$ 的边。

第 $(n + 1)$ 到第 $(n + m)$ 行，每行有三个用空格隔开的整数 $x, y, z$，代表一次救济粮的发放是从 $x$ 到 $y$ 路径上的每栋房子发放了一袋 $z$ 类型的救济粮。

输出格式

输出 $n$ 行，每行一个整数，第 $i$ 行的整数代表 $i$ 号房屋存放最多的救济粮的种类，如果有多种救济粮都是存放最多的，输出种类编号最小的一种。

如果某座房屋没有救济粮，则输出 $0$。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
5 3
1 2
3 1
3 4
5 3
2 3 3
1 5 2
3 3 3

样例输出 #1

1
2
3
4
5
2
3
3
0
2

提示

  • 对于 $20%$ 的数据，保证 $n, m \leq 100$。
  • 对于 $50%$ 的数据，保证 $n, m \leq 2 \times 10^3$。
  • 对于 $100%$ 测试数据，保证 $1 \leq n, m \leq 10^5$，$1 \leq a,b,x,y \leq n$，$1 \leq z \leq 10^5$。

分析：

考虑暴力：可以树上差分，将单次区间修改变为四次单点修改，即$[x,y]$的修改对应$x,y$的单点加和$lca(x,y),fa_{lca(x,y)}$的单点减，最后求答案时从下往上前缀和即可。

但是这样会超时，而这种算法的瓶颈是最后的数组加，于是可以使用权值线段树的合并优化这个过程。在每个节点上新建一个权值线段树，下标为救济粮的种类，按照上面的思路，最后进行线段树合并即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
#include<bits/stdc++.h>
using namespace std;

const int N=1e5+5,MAX=1e5;
int n,m;

int h[N],to[100*N],ne[100*N];//树部分
int idx;
void addedge(int u,int v){
    to[++idx]=v;
    ne[idx]=h[u];
    h[u]=idx;
}

int anc[N][20],dep[N];//LCA部分
void dfs(int u,int fa){
    anc[u][0]=fa;
    dep[u]=dep[fa]+1;
    for(int i=h[u];i;i=ne[i]){
        if(to[i]!=fa){
            dfs(to[i],u);
        }
    }
}

void init(){
    for(int i=1;i<=17;i++){
        for(int j=1;j<=n;j++){
            anc[j][i]=anc[anc[j][i-1]][i-1];
        }
    }
}

int lca(int x,int y){
    if(dep[x]<dep[y])swap(x,y);
    for(int i=17;i>=0;i--){
        if(dep[anc[x][i]]>=dep[y])x=anc[x][i];
    }
    if(x==y)return x;
    for(int i=17;i>=0;i--){
        if(anc[x][i]!=anc[y][i])x=anc[x][i],y=anc[y][i];
    }
    return anc[x][0];
}


struct node{//线段树部分
    int l,r;
    int mx,mx_sum;
};

node tr[N*100];int idx_tr;

void pushup(int u){
    if(!tr[u].l){
        tr[u].mx=tr[tr[u].r].mx;
        tr[u].mx_sum=tr[tr[u].r].mx_sum;
    }
    if(!tr[u].r){
        tr[u].mx=tr[tr[u].l].mx;
        tr[u].mx_sum=tr[tr[u].l].mx_sum;
    }
    if(tr[tr[u].l].mx_sum>=tr[tr[u].r].mx_sum){
        tr[u].mx=tr[tr[u].l].mx;
        tr[u].mx_sum=tr[tr[u].l].mx_sum;
    }
    else{
        tr[u].mx=tr[tr[u].r].mx;
        tr[u].mx_sum=tr[tr[u].r].mx_sum;
    }
}

void change(int &u,int l,int r,int x,int k){
    if(!u)u=++idx_tr;
    if(l==r){
        tr[u].mx=x;
        tr[u].mx_sum+=k;
        return;
    }
    int mid=l+r>>1;
    if(x<=mid)change(tr[u].l,l,mid,x,k);
    else change(tr[u].r,mid+1,r,x,k);
    pushup(u);
}

int merge(int x,int y,int l,int r){
    if(!x||!y)return x|y;
    if(l==r){
        tr[y].mx_sum+=tr[x].mx_sum;
        return y;
    }
    int mid=l+r>>1;
    tr[y].l=merge(tr[x].l,tr[y].l,l,mid);
    tr[y].r=merge(tr[x].r,tr[y].r,mid+1,r);
    pushup(y);
    return y;
}

int ans[N];
void get(int u,int fa){
    for(int i=h[u];i;i=ne[i]){
        if(to[i]!=fa){
            get(to[i],u);
            u=merge(to[i],u,1,MAX);
        }
    }
    ans[u]=tr[u].mx;
    if(tr[u].mx_sum==0)ans[u]=0;
}

int main(){
    cin >> n >> m;
    for(int i=1;i<n;i++){
        int a,b;
        cin >> a >> b;
        addedge(a,b);
        addedge(b,a);
    }
    dfs(1,0);
    init();
    idx_tr=n;
    for(int i=1;i<=m;i++){
        int x,y,z;
        cin >> x >> y >> z;
        int l=lca(x,y);
        change(x,1,MAX,z,1);
        change(y,1,MAX,z,1);
        change(l,1,MAX,z,-1);
        change(anc[l][0],1,MAX,z,-1);
    }
    get(1,0);
    for(int i=1;i<=n;i++){
        cout << ans[i] << endl;
    }
    return 0;
}

例题6：洛谷P5298 [PKUWC2018] Minimax（线段树合并优化树形dp）

[PKUWC2018] Minimax

题目描述

小 $C$ 有一棵 $n$ 个结点的有根树，根是 $1$ 号结点，且每个结点最多有两个子结点。

定义结点 $x$ 的权值为：

1.若 $x$ 没有子结点，那么它的权值会在输入里给出，保证这类点中每个结点的权值互不相同。

2.若 $x$ 有子结点，那么它的权值有 $p_x$ 的概率是它的子结点的权值的最大值，有 $1-p_x$ 的概率是它的子结点的权值的最小值。

现在小 $C$ 想知道，假设 $1$ 号结点的权值有 $m$ 种可能性，权值第 $i$ 小的可能性的权值是 $V_i$，它的概率为 $D_i(D_i>0)$，求：

$$\sum_{i=1}^{m}i\cdot V_i\cdot D_i^2$$

你需要输出答案对 $998244353$ 取模的值。

输入格式

第一行一个正整数 $n$；

第二行 $n$ 个整数，第 $i$ 个整数表示第 $i$ 个结点的父亲的编号，其中第 $1$ 个结点的父亲为 $0$；

第三行 $n$ 个整数，若第 $i$ 个结点没有子结点，则第 $i$ 个数为它的权值，否则第 $i$ 个数为 $p_i\cdot 10000$，保证 $p_i\cdot 10000$ 是个正整数。

输出格式

输出答案。

样例 #1

样例输入 #1

1
2
3
3
0 1 1
5000 1 2

样例输出 #1

1
748683266

提示

样例解释

1号结点的权值有 $\frac{1}{2}$ 的概率是 $1$，有 $\frac{1}{2}$ 的概率是 $2$，所以答案是 $\frac{5}{4}$。

数据范围

  • 对于 $10%$ 的数据，有 $1\leq n\leq 20$；
  • 对于 $20%$ 的数据，有 $1\leq n\leq 400$；
  • 对于 $40%$ 的数据，有 $1\leq n\leq 5000$；
  • 对于 $60%$ 的数据，有 $1\leq n\leq 10^5$；
  • 另有 $10%$ 的数据保证树的形态随机；
  • 对于 $100%$ 的数据，有 $1\leq n\leq 3\times 10^5$，$1\leq w_i\leq 10^9$。

对于所有数据，满足 $0 < p_i \cdot 10000 < 10000$，所以易证明所有叶子的权值都有概率被根取到。

线段树分裂

线段树不仅支持合并，也同样支持分裂。

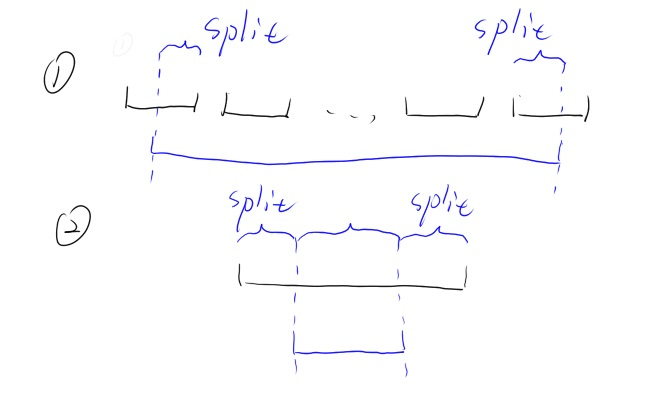
假设我们需要将权值线段树$T$分为$\le k$的部分$T_1$和$>k$的部分$T_2$。原树上的点可分为两类，对于第一类的点，其子树内同时含有两部分的叶子，则其在$T_!$，$T_2$中同时出现；否则，其只会在$T_1$或$T_2$中出现。我们只遍历原树上的第一类点，将其属于第二类的儿子挂在$T_1$或$T_2$中，再更新其在$T_1$及$T_2$中的信息即可。由于第一类点不超过$O(\log n)$个，因此遍历、新建的节点数为$O(\log n)$级别。

1
2
3
4
5
6
7
8
9
void split(int x,int &y,int k){
    if(!x)return;
    y=++cnt;//新树中的点
    int sizel=tr[tr[x].l].sz;
    if(k<sizel)swap(tr[x].r,tr[y].r),split(tr[x].l,tr[y].l,k);//把右儿子加到新树里
    else if(k==sizel)swap(tr[x].r,tr[y].r);//把右儿子加到新树里
    else split(tr[x].r,tr[y].r,k-sizel);
    pushup(x),pushup(y);
}

例题7：洛谷P2824 [HEOI2016/TJOI2016] 排序（线段树分裂）

[HEOI2016/TJOI2016] 排序

题目描述

在 $2016$ 年，佳媛姐姐喜欢上了数字序列。因而她经常研究关于序列的一些奇奇怪怪的问题，现在她在研究一个难题，需要你来帮助她。

这个难题是这样子的：给出一个 $1$ 到 $n$ 的排列，现在对这个排列序列进行 $m$ 次局部排序，排序分为两种：

  • 0 l r 表示将区间 $[l,r]$ 的数字升序排序
  • 1 l r 表示将区间 $[l,r]$ 的数字降序排序

注意，这里是对下标在区间 $[l,r]$ 内的数排序。
最后询问第 $q$ 位置上的数字。

输入格式

输入数据的第一行为两个整数 $n$ 和 $m$，$n$ 表示序列的长度，$m$ 表示局部排序的次数。

第二行为 $n$ 个整数，表示 $1$ 到 $n$ 的一个排列。

接下来输入 $m$ 行，每一行有三个整数 $\text{op},l,r$，$\text{op}$ 为 $0$ 代表升序排序，$\text{op}$ 为 $1$ 代表降序排序, $l,r$ 表示排序的区间。

最后输入一个整数 $q$，表示排序完之后询问的位置

输出格式

输出数据仅有一行，一个整数，表示按照顺序将全部的部分排序结束后第 $q$ 位置上的数字。

样例 #1

样例输入 #1

1
2
3
4
5
6
6 3
1 6 2 5 3 4
0 1 4
1 3 6
0 2 4
3

样例输出 #1

1
5

提示

河北省选2016第一天第二题。

对于 $30%$ 的数据，$n,m\leq 1000$

对于 $100%$ 的数据，$n,m\leq 10^5$，$1\leq q\leq n$

分析：

可以将序列划分为多个连续段，每个连续段内序列单调，使用权值线段树维护，初始时每个元素位于单独的连续段内。当进行操作时，可以将多个连续段拆分合并成新的连续段，使用set维护连续段，每次二分查找连续段并进行操作。

操作时，可能遇到特殊情况：

对于第一种情况，二分左右端点，分裂左端点的右半部分和右端点的左半部分对应的权值线段树，与中间部分合并即可。

对于第二种情况，把连续段分裂成三部分，取中间部分即可。

注意，对于每种情况，要分升序和降序两种情况讨论。

代码：(未AC)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
#include<bits/stdc++.h>
using namespace std;

const int N=1e5+5;
struct node{
    int l,r;
    int sz;
    void clear(){
        l=r=sz=0;
    }
};
struct data{
    int l,r;
    bool flag;
    int tr;
    void clear(){
        l=r=flag=0;
    }
    bool operator<(const data x)const{
        return r<x.r;
    }
};
set<data>seq;
node tr[100*N];
int idx;
data newq(int l,int r,bool flag,int x){
    data t;
    t.l=l,t.r=r,t.flag=flag,t.tr=x;
    return t;
}

int n,m;
int a[N];
void pushup(int u){
    tr[u].sz=tr[tr[u].l].sz+tr[tr[u].r].sz;
}

void change(int &u,int l,int r,int x,int k){
    if(!u)u=++idx;
    if(l==r){
        tr[u].sz+=k;
        return;
    }
    int mid=l+r>>1;
    if(x<=mid)change(tr[u].l,l,mid,x,k);
    else change(tr[u].r,mid+1,r,x,k);
    pushup(u);
}

int merge(int x,int y,int l,int r){
    if(!x||!y)return x|y;
    if(l==r){
        tr[y].sz+=tr[x].sz;
        return y;
    }
    int mid=l+r>>1;
    tr[y].l=merge(tr[x].l,tr[y].l,l,mid);
    tr[y].r=merge(tr[x].r,tr[y].r,mid+1,r);
    pushup(y);
    return y;
}

void split(int x,int &y,int k){
    if(!x)return;
    y=++idx;
    if(k<tr[tr[x].l].sz)swap(tr[x].r,tr[y].r),split(tr[x].l,tr[y].l,k); 
    else if(k==tr[tr[x].l].sz)swap(tr[x].r,tr[y].r);
    else split(tr[x].r,tr[y].r,k-tr[tr[x].l].sz);
    pushup(x),pushup(y);
}
int ans[N],cnt;
void out(bool opt,int u,int l,int r){
    if(!u)return;
    if(l==r){
        ans[++cnt]=l;
        return;
    }
    int mid=l+r>>1;
    if(opt==0){
        out(opt,tr[u].l,l,mid);
        out(opt,tr[u].r,mid+1,r);
    }
    else{
        out(opt,tr[u].r,mid+1,r);
        out(opt,tr[u].l,l,mid);
    }
}

int main(){
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        cin >> a[i];
        int x=0;
        change(x,1,n,a[i],1);
        seq.insert(newq(i,i,0,x));
    }
    
    for(int i=1;i<=m;i++){
        int op,l,r;
        cin >> op >> l >> r;
        auto left=seq.lower_bound(newq(0,l,0,0));
        int res=0;
        bool fflag=0;
        while(left!=seq.end()&&left->l<=r){
            auto now=*left;
            auto tt=left;tt++;
            seq.erase(left);left=tt;
            if(now.l>=l&&now.r<=r){//完全包含
                res=merge(now.tr,res,1,n);
            }
            else if(now.l<=l&&now.r>=r){//取中间
                if(op==now.flag){//符号相同，不用改，放回去
                    seq.insert(now);
                    goto end;
                }
                else if(now.flag){//符号不同，拆成三段，分开考虑
                    int tmp=0;
                    split(now.tr,tmp,now.r-r);
                    split(tmp,res,r-l+1);
                    swap(tmp,res);swap(now.tr,tmp);
                    if(tr[now.tr].sz)seq.insert(newq(now.l,l-1,now.flag,now.tr));
                    if(tr[tmp].sz)seq.insert(newq(r+1,now.r,now.flag,tmp));
                }
                else{
                    int tmp=0;
                    split(now.tr,tmp,l-now.l);
                    split(tmp,res,r-l+1);
                    swap(tmp,res);
                    swap(now.tr,tmp);
                    if(tr[tmp].sz)seq.insert(newq(now.l,l-1,now.flag,tmp));
                    if(tr[now.tr].sz)seq.insert(newq(r+1,now.r,now.flag,now.tr));
                }
                seq.insert(newq(l,r,op,res));
                goto end;
            }
            else if(now.l<l){//取右边
                if(now.flag){
                    int tmp=0;
                    split(now.tr,tmp,now.r-l+1);
                    res=merge(now.tr,res,1,n);
                    if(tr[tmp].sz)seq.insert(newq(now.l,l-1,now.flag,tmp));
                }
                else{
                    int tmp=0;
                    split(now.tr,tmp,l-now.l);
                    res=merge(tmp,res,1,n);
                    if(tr[now.tr].sz)seq.insert(newq(now.l,l-1,now.flag,now.tr));
                }
            }
            else if(now.r>r){//取左边
                if(now.flag){
                    int tmp=0;
                    split(now.tr,tmp,now.r-r);
                    res=merge(tmp,res,1,n);
                    if(tr[now.tr].sz)seq.insert(newq(r+1,now.r,now.flag,now.tr));
                }
                else{
                    int tmp=0;
                    split(now.tr,tmp,r-now.l+1);
                    res=merge(now.tr,res,1,n);
                    if(tr[tmp].sz)seq.insert(newq(r+1,now.r,now.flag,tmp));
                }
            }
        }
        seq.insert(newq(l,r,op,res));
        end:;
    }
    for(auto x:seq){
        out(x.flag,x.tr,1,n);
    }
    int q;
    cin >> q;
    cout << ans[q];
    return 0;
}

可持久化线段树（主席树）

考虑这样一个问题：给定长度为$n$的序列$a$和$q$次命令，每次命令形如：

  • 将$a_i$加上$x$。
  • 查询第$i$次操作结束后的$[l,r]$的和。

首先，若第$2$类操作的$i$总等于当前操作的次数，可直接$O(\log n)$地用线段树维护。

但是，现在我们要访问线段树的任意历史版本。注意到，每次单点修改后，只有$O(\log n)$个节点的权值发生了改变。我们考虑只新建$O(\log n)$个点，而非$O(n)$地全盘推倒重建。具体来说，对于被修改的非叶节点$x$，设$x$的左儿子为$p$。若$p$也被修改，则建立一个与$p$对应的新点$p’$，将$x’$的左儿子设为$p’$，并向$p’$递归处理；否则，$x’$的左儿子仍为$p$。右儿子的处理是相同的。

具体实现：

  1. 将当前点复制一遍
  2. 如果当前点是叶节点，直接修改；若不是，分情况向下遍历：
    • 若要修改的点在左子树，遍历左儿子，新点的右儿子为原点的右儿子
    • 若要修改的点在右子树，遍历右儿子，新点的左儿子为原点的左儿子
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
struct node{
    int l,r;
    int sum;
}tr[N];
int idx;

int copy(int u){
    tr[++idx]=tr[u];
    return idx;
}

int change(int u,int l,int r,int x,int k){
    u=copy(u);
    if(l==r){
        tr[u].sum+=k;
        return u;
    }
    int mid=l+r>>1;
    if(x<=mid)tr[u].l=change(tr[u].l,l,mid,x,k);
    else tr[u].r=change(tr[u].r,mid+1,r,x,k);
    pushup(u);
    return u;
}

例题8：洛谷P3919 【模板】可持久化线段树 1（可持久化数组）

【模板】可持久化线段树 1（可持久化数组）

题目背景

UPDATE : 最后一个点时间空间已经放大

2021.9.18 增添一组 hack 数据 by @panyf

标题即题意

有了可持久化数组，便可以实现很多衍生的可持久化功能（例如：可持久化并查集）

题目描述

如题，你需要维护这样的一个长度为 $ N $ 的数组，支持如下几种操作

  1. 在某个历史版本上修改某一个位置上的值

  2. 访问某个历史版本上的某一位置的值

此外，每进行一次操作（对于操作2，即为生成一个完全一样的版本，不作任何改动），就会生成一个新的版本。版本编号即为当前操作的编号（从1开始编号，版本0表示初始状态数组）

输入格式

输入的第一行包含两个正整数 $ N, M $， 分别表示数组的长度和操作的个数。

第二行包含$ N $个整数，依次为初始状态下数组各位的值（依次为 $ a_i $，$ 1 \leq i \leq N $）。

接下来$ M $行每行包含3或4个整数，代表两种操作之一（$ i $为基于的历史版本号）：

  1. 对于操作1，格式为$ v_i \ 1 \ {loc}_i \ {value}i $，即为在版本$ v_i $的基础上，将 $ a{loc_i} $ 修改为 $ {value}_i $。

  2. 对于操作2，格式为$ v_i \ 2 \ {loc}i $，即访问版本$ v_i $中的 $ a{loc_i} $的值，注意：**生成一样版本的对象应为 $v_i$**。

输出格式

输出包含若干行，依次为每个操作2的结果。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
9
10
11
12
5 10
59 46 14 87 41
0 2 1
0 1 1 14
0 1 1 57
0 1 1 88
4 2 4
0 2 5
0 2 4
4 2 1
2 2 2
1 1 5 91

样例输出 #1

1
2
3
4
5
6
59
87
41
87
88
46

提示

数据规模：

对于30%的数据：$ 1 \leq N, M \leq {10}^3 $

对于50%的数据：$ 1 \leq N, M \leq {10}^4 $

对于70%的数据：$ 1 \leq N, M \leq {10}^5 $

对于100%的数据：$ 1 \leq N, M \leq {10}^6, 1 \leq {loc}_i \leq N, 0 \leq v_i < i, -{10}^9 \leq a_i, {value}_i \leq {10}^9$

经测试，正常常数的可持久化数组可以通过，请各位放心

数据略微凶残，请注意常数不要过大

另，此题I/O量较大，如果实在TLE请注意I/O优化

询问生成的版本是指你访问的那个版本的复制

样例说明：

一共11个版本，编号从0-10，依次为：

* 0 : 59 46 14 87 41

* 1 : 59 46 14 87 41

* 2 : 14 46 14 87 41

* 3 : 57 46 14 87 41

* 4 : 88 46 14 87 41

* 5 : 88 46 14 87 41

* 6 : 59 46 14 87 41

* 7 : 59 46 14 87 41

* 8 : 88 46 14 87 41

* 9 : 14 46 14 87 41

* 10 : 59 46 14 87 91

分析：

模板题，新建一个数组记录每个版本的根。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include<bits/stdc++.h>
using namespace std;

const int N=1e6+5;

int n,m;
int a[N];

struct node{
    int l,r;
    int sum;
};
node tr[50*N];
int idx;

void pushup(int u){
    tr[u].sum=tr[tr[u].l].sum+tr[tr[u].r].sum;
}

void build(int &u,int l,int r){
    if(!u)u=++idx;
    if(l==r){
        tr[u].sum=a[l];
        return;
    }
    int mid=l+r>>1;
    build(tr[u].l,l,mid);
    build(tr[u].r,mid+1,r);
    pushup(u);
}

int root[N],cnt;

int copy(int u){
    tr[++idx]=tr[u];
    return idx;
}

int change(int u,int l,int r,int x,int k){
    u=copy(u);
    if(l==r){
        tr[u].sum=k;
        return u;
    }
    int mid=l+r>>1;
    if(x<=mid)tr[u].l=change(tr[u].l,l,mid,x,k);
    else tr[u].r=change(tr[u].r,mid+1,r,x,k);
    pushup(u);
    return u;
}

int find(int u,int l,int r,int x){
    if(l==r)return tr[u].sum;
    int mid=l+r>>1;
    if(x<=mid)return find(tr[u].l,l,mid,x);
    return find(tr[u].r,mid+1,r,x);
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        cin >> a[i];
    }
    build(root[cnt],1,n);
    for(int i=1;i<=m;i++){
        int ver,op,loc;
        cin >> ver >> op >> loc;
        if(op==1){
            int val;
            cin >> val;
            root[++cnt]=change(root[ver],1,n,loc,val);
        }
        else{
            cout << find(root[ver],1,n,loc) << endl;
            root[++cnt]=root[ver];
        }
    }
    return 0;
}

例题9：洛谷P3834 【模板】可持久化线段树 2（静态区间第$k$大）

【模板】可持久化线段树 2

题目背景

这是个非常经典的可持久化权值线段树入门题——静态区间第 $k$ 小。

数据已经过加强，请使用可持久化权值线段树。同时请注意常数优化。

题目描述

如题，给定 $n$ 个整数构成的序列 $a$，将对于指定的闭区间 $[l, r]$ 查询其区间内的第 $k$ 小值。

输入格式

第一行包含两个整数，分别表示序列的长度 $n$ 和查询的个数 $m$。
第二行包含 $n$ 个整数，第 $i$ 个整数表示序列的第 $i$ 个元素 $a_i$。
接下来 $m$ 行每行包含三个整数 $ l, r, k$ , 表示查询区间 $[l, r]$ 内的第 $k$ 小值。

输出格式

对于每次询问，输出一行一个整数表示答案。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
5 5
25957 6405 15770 26287 26465 
2 2 1
3 4 1
4 5 1
1 2 2
4 4 1

样例输出 #1

1
2
3
4
5
6405
15770
26287
25957
26287

提示

样例 1 解释

$n=5$，数列长度为 $5$，数列从第一项开始依次为${25957, 6405, 15770, 26287, 26465}$。

  • 第一次查询为 $[2, 2]$ 区间内的第一小值，即为 $6405$。
  • 第二次查询为 $[3, 4]$ 区间内的第一小值，即为 $15770$。
  • 第三次查询为 $[4, 5]$ 区间内的第一小值，即为 $26287$。
  • 第四次查询为 $[1, 2]$ 区间内的第二小值，即为 $25957$。
  • 第五次查询为 $[4, 4]$ 区间内的第一小值，即为 $26287$。

数据规模与约定

  • 对于 $20%$ 的数据，满足 $1 \leq n,m \leq 10$。
  • 对于 $50%$ 的数据，满足 $1 \leq n,m \leq 10^3$。
  • 对于 $80%$ 的数据，满足 $1 \leq n,m \leq 10^5$。
  • 对于 $100%$ 的数据，满足 $1 \leq n,m \leq 2\times 10^5$，$|a_i| \leq 10^9$，$1 \leq l \leq r \leq n$，$1 \leq k \leq r - l + 1$。

形式化题面：

给定$n(n \le 2 \times 10^5)$个整数构成的序列$a$和$m(m \le 2\times 10^5 )$次询问，每次给定$l,r,k$，查询指定的闭区间$[l,r]$内的第$k$小值。

分析：

可以发现，这道题与例题例题4（查询序列第$k$小）类似，但是要求查询区间的第$k$小，考虑如何转换。

可以建立序列的所有前缀的权值线段树，即主席树的$n$次单点修改，每次询问时在$l-1,r$两棵线段树上同时二分，即可得出答案。

具体来说，同时二分两棵线段树，设$l-1,r$的左子树的权值分别为$c,c’$，则当$c’-c \ge k$ 时，两棵树同时向左儿子遍历，否则向右儿子遍历。

由于值域很大，需要进行离散化。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include<bits/stdc++.h>
using namespace std;

const int N=2e5+5,MAX=2e9+1;

int num[N],num_cnt;
int find(int x){
    int l=1,r=num_cnt;
    while(l<r){
        int mid=l+r>>1;
        if(x<=num[mid])r=mid;
        else l=mid+1;
    }
    return l;
}

int n,m;
int a[N];

struct node{
    int l,r;
    int sz;
}tr[50*N];
int idx;

int root[N],cnt;

void pushup(int u){
    tr[u].sz=tr[tr[u].l].sz+tr[tr[u].r].sz;
}

int copy(int u){
    tr[++idx]=tr[u];
    return idx;
}

int change(int u,int l,int r,int x){
    u=copy(u);
    if(l==r){
        tr[u].sz++;
        return u;
    }
    int mid=l+r>>1;
    if(x<=mid)tr[u].l=change(tr[u].l,l,mid,x);
    else tr[u].r=change(tr[u].r,mid+1,r,x);
    pushup(u);
    return u;
}

int query(int ul,int ur,int l,int r,int k){
    if(l==r){
        return l;
    }
    int sz=tr[tr[ur].l].sz-tr[tr[ul].l].sz;
    int mid=l+r>>1;
    if(sz>=k)return query(tr[ul].l,tr[ur].l,l,mid,k);
    return query(tr[ul].r,tr[ur].r,mid+1,r,k-sz);
}

int main(){
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        cin >> a[i];
        num[++num_cnt]=a[i];
    }
    sort(num+1,num+num_cnt+1);
    num_cnt=unique(num+1,num+num_cnt+1)-(num+1);
    for(int i=1;i<=n;i++){
        root[++cnt]=change(root[i-1],1,MAX,find(a[i]));
    }
    for(int i=1;i<=m;i++){
        int l,r,k;
        cin >> l >> r >> k;
        cout << num[query(root[l-1],root[r],1,MAX,k)] << endl;
    }
    return 0;
}

带懒标记线段树的可持久化

每次如果要下放标记，就新建两个节点，并继续递归相应点。

区间mex问题

例题10：洛谷P4137 Rmq Problem / mex

Rmq Problem / mex

题目描述

有一个长度为 $n$ 的数组 ${a_1,a_2,\ldots,a_n}$。

$m$ 次询问，每次询问一个区间内最小没有出现过的自然数。

输入格式

第一行，两个正整数 $n,m$。
第二行，$n$ 个非负整数 $a_1, a_2, \ldots , a_n$。
接下来 $m$ 行，每行两个正整数 $l,r$，表示一次询问。

输出格式

输出 $m$ 行，每行一个数，依次表示每个询问的答案。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
5 5
2 1 0 2 1
3 3
2 3
2 4
1 2
3 5

样例输出 #1

1
2
3
4
5
1
2
3
0
3

提示

对于 $30%$ 的数据：$1\leq n,m\leq 1000$。
对于 $100%$ 的数据：$1\leq n,m\leq 2\times {10}^5$，$1\leq l\leq r\leq n$，$0\leq a_i\leq 2\times 10^5$。

分析：

考虑对于每个节点不再维护区间数的数量，维护$last_i$表示$i$上一次出现的位置，则对于每次询问$[l,r]$，只需查询$r$上$last$小于$l$的最小值即可。

接下来考虑如何查找，对于一个节点$u$，若左子树任意点的$last_i \le l$ 则向右递归，否则向左递归，直到走到叶节点。

考虑如何判断$last_i \le l$，可以维护所有$last$的最小值，若最小值$\le l$即可。

考虑如何维护最小值，设当前已知第$i-1$个线段树，则第$i$个线段树的$last_{a_i}$会变成$i$，相当于对$i$进行了一次单点修改。

注意到当$a_i>n$时，$a_i$一定不会被取到，因此直接忽略即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<bits/stdc++.h>
using namespace std;

const int N=2e5+5;

int n,m;
int a[N];

int root[N],cnt;

struct node{
    int l,r;
    int minn;
}tr[N*50];

int idx;

void pushup(int u){
    tr[u].minn=min(tr[tr[u].l].minn,tr[tr[u].r].minn);
}

int copy(int u){
    tr[++idx]=tr[u];
    return idx;
}

int change(int u,int l,int r,int x,int k){
    u=copy(u);
    if(l==r){
        tr[u].minn=k;
        return u;
    }
    int mid=l+r>>1;
    if(x<=mid)tr[u].l=change(tr[u].l,l,mid,x,k);
    else tr[u].r=change(tr[u].r,mid+1,r,x,k);
    pushup(u);
    return u;
}

int query(int u,int l,int r,int lim){
    if(l==r){
        return l;
    }
    int mid=l+r>>1;
    if(tr[tr[u].l].minn<lim) return query(tr[u].l,l,mid,lim);
    return query(tr[u].r,mid+1,r,lim);
}

int main(){
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        cin >> a[i];
        if(a[i]<=n)root[i]=change(root[i-1],0,n,a[i],i);
        else root[i]=root[i-1];
    }
    for(int i=1;i<=m;i++){
        int l,r;
        cin >> l >> r;
        cout << query(root[r],0,n,l) << endl;
    }
    return 0;
}

例题11：洛谷CF464E The Classic Problem/Codeforces 464E

The Classic Problem

题面翻译

给定一张 $n$ 个点，$m$ 条边的无向图，每条边的边权为 $2^{x_i}$，求 $s$ 到 $t$ 的最短路，结果对 $10^9+7$ 取模。

$n, m, x \leq 10^5$。

题目描述

You are given a weighted undirected graph on $ n $ vertices and $ m $ edges. Find the shortest path from vertex $ s $ to vertex $ t $ or else state that such path doesn’t exist.

输入格式

The first line of the input contains two space-separated integers — $ n $ and $ m $ ( $ 1<=n<=10^{5} $ ; $ 0<=m<=10^{5} $ ).

Next $ m $ lines contain the description of the graph edges. The $ i $ -th line contains three space-separated integers — $ u_{i} $ , $ v_{i} $ , $ x_{i} $ ( $ 1<=u_{i},v_{i}<=n $ ; $ 0<=x_{i}<=10^{5} $ ). That means that vertices with numbers $ u_{i} $ and $ v_{i} $ are connected by edge of length $ 2^{x_{i}} $ (2 to the power of $ x_{i} $ ).

The last line contains two space-separated integers — the numbers of vertices $ s $ and $ t $ .

The vertices are numbered from $ 1 $ to $ n $ . The graph contains no multiple edges and self-loops.

输出格式

In the first line print the remainder after dividing the length of the shortest path by $ 1000000007 (10^{9}+7) $ if the path exists, and -1 if the path doesn’t exist.

If the path exists print in the second line integer $ k $ — the number of vertices in the shortest path from vertex $ s $ to vertex $ t $ ; in the third line print $ k $ space-separated integers — the vertices of the shortest path in the visiting order. The first vertex should be vertex $ s $ , the last vertex should be vertex $ t $ . If there are multiple shortest paths, print any of them.

样例 #1

样例输入 #1

1
2
3
4
5
6
4 4
1 4 2
1 2 0
2 3 0
3 4 0
1 4

样例输出 #1

1
2
3
3
4
1 2 3 4

样例 #2

样例输入 #2

1
2
3
4
5
4 3
1 2 4
2 3 5
3 4 6
1 4

样例输出 #2

1
2
3
112
4
1 2 3 4

样例 #3

样例输入 #3

1
2
3
4
4 2
1 2 0
3 4 1
1 4

样例输出 #3

1
-1

提示

A path from vertex $ s $ to vertex $ t $ is a sequence $ v_{0} $ , …, $ v_{k} $ , such that $ v_{0}=s $ , $ v_{k}=t $ , and for any $ i $ from 0 to $ k-1 $ vertices $ v_{i} $ and $ v_{i+1} $ are connected by an edge.

The length of the path is the sum of weights of edges between $ v_{i} $ and $ v_{i+1} $ for all $ i $ from 0 to $ k-1 $ .

The shortest path from $ s $ to $ t $ is the path which length is minimum among all possible paths from $ s $ to $ t $ .

分析：

这是一道最短路的题，但是发现边权非常大，无法直接计算，因此需要使用高精度。但是如果直接使用高精度，时间复杂度很大，于是考虑用权值线段树实现高精度。

考虑需要进行的操作：

  1. 比较两个二进制数的大小
  2. 进行单点修改，单点查询
  3. 设为无穷大$\inf$
  4. 将一个节点的$dis$复制到另一节点

对于第一个操作，可以在每个节点维护一个哈希值，比较时使用线段树二分，若左儿子的哈希值不同，则向左儿子递归，否则向右儿子递归，直到走到根节点，判断两棵树的这一位是$0$还是$1$即可。

对于第二个操作，正常处理即可。

对于第三个操作，由于$n$最大为$10^5$，因此只需将$\inf$设为大于$10^5\times\log_2 10^5 \approx 1660964$的数，即$2\times 10^5$即可。

对于第四个操作，只需将上面的操作可持久化即可。

平衡树

全称“平衡二叉搜索树”，常见的类型有：

  1. splay
  2. treap
  3. AVL Tree
  4. Red Black Tree
  5. Scape Goat Tree
  6. Weight Balanced Leafy Tree（特殊结构）

二叉搜索树

性质：一个节点$x$左子树所有点的关键字都比$x$的关键字小，右子树的所有点的关键字都比$x$的关键字大。

treap

基础知识略

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
#include <bits/stdc++.h>
using namespace std; 

const int N=100010,INF=1e8;

int n;
struct Node{
    int l,r;
    int key,val;
    int cnt,size;
}tr[N];
int root,idx;

void pushup(int p){
    tr[p].size=tr[tr[p].l].size+tr[tr[p].r].size+tr[p].cnt;
}

int get_node(int key){
    tr[++idx].key=key;
    tr[idx].val=rand();
    tr[idx].cnt=tr[idx].size=1;
    return idx;
}

void build(){
    get_node(-INF),get_node(INF);
    root=1,tr[1].r=2;
    pushup(root);
}

void zig(int &p){
    int q=tr[p].l;
    tr[p].l=tr[q].r,tr[q].r=p,p=q;
    pushup(tr[p].r),pushup(p);
}

void zag(int &p){
    int q=tr[p].r;
    tr[p].r=tr[q].l,tr[q].l=p,p=q;
    pushup(tr[p].l),pushup(p);
}

void insert(int &p,int key){
    if(!p)p=get_node(key);
    else if(tr[p].key==key)tr[p].cnt++;
    else if(tr[p].key>key){
        insert(tr[p].l,key);
        if(tr[tr[p].l].val>tr[p].val)zig(p);
    }
    else{
        insert(tr[p].r,key);
        if(tr[tr[p].r].val>tr[p].val)zag(p);
    }
    pushup(p);
}

void remove(int &p,int key){
    if(!p)return;
    if(tr[p].key==key){
        if(tr[p].cnt>1)tr[p].cnt--;
        else if(tr[p].l||tr[p].r){
            if(!tr[p].r||tr[tr[p].l].val>tr[tr[p].r].val){
                zig(p);
                remove(tr[p].r,key);
            }
            else{
                zag(p);
                remove(tr[p].l,key);
            }
        }
        else p=0;
    }
    else if(tr[p].key>key)remove(tr[p].l,key);
    else remove(tr[p].r,key);
    pushup(p);
}

int get_rank_by_key(int p,int key){
    if(!p)return 0;
    if(tr[p].key==key)return tr[tr[p].l].size+1;
    if(tr[p].key>key)return get_rank_by_key(tr[p].l,key);
    return tr[tr[p].l].size+tr[p].cnt+get_rank_by_key(tr[p].r,key);
}

int get_key_by_rank(int p,int rank){
    if(!p)return INF;
    if(tr[tr[p].l].size>=rank)return get_key_by_rank(tr[p].l,rank);
	if(tr[tr[p].l].size+tr[p].cnt>=rank)return tr[p].key;
    return get_key_by_rank(tr[p].r,rank-tr[tr[p].l].size-tr[p].cnt);
}

int get_prev(int p,int key){
    if(!p)return -INF;
    if(tr[p].key>=key)return get_prev(tr[p].l,key);
    return max(tr[p].key,get_prev(tr[p].r,key));
}

int get_next(int p,int key){
    if(!p)return INF;
    if(tr[p].key<=key)return get_next(tr[p].r,key);
    return min(tr[p].key,get_next(tr[p].l,key));
}

int main()
{
    build();
    scanf("%d",&n);
    while(n--){
        int opt,x;
        scanf("%d%d",&opt,&x);
        if(opt==1)insert(root,x);
        else if(opt==2)remove(root,x);
        else if(opt==3)printf("%d\n",get_rank_by_key(root,x)-1);
        else if(opt==4)printf("%d\n",get_key_by_rank(root,x+1));
        else if(opt==5)printf("%d\n",get_prev(root,x));
        else printf("%d\n",get_next(root,x));
    }
    return 0;
}

无旋treap

核心函数：

  • split(x,a,b,k)：当前为x，将树分为左边大小为k的两棵树a,b，直接递归处理，若k小于等于左儿子的大小，递归处理左儿子，否则处理右儿子的a-s-1（s为左儿子大小）。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    void split(int now,int &a,int &b,int k){
    	if(now==0){a=0;b=0;return;}
    	pushdown(now);
    	if(si[t[now][0]]<k){
    		a=now;
    		split(t[now][1],t[now][1],b,k-si[t[now][0]]-1);
    	}
    	else{
    		b=now;
    		split(t[now][0],a,t[now][0],k);
    	}
    	pushup(now);
    }

  • merge

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    int merge(int a,int b){
    	if(!a||!b) return a+b;
    	if(key[a]<=key[b]){
    		pushdown(a);
    		t[a][1]=merge(t[a][1],b);
    		pushup(a);
    		return a;
    	}
    	else{
    		pushdown(b);
    		t[b][0]=merge(a,t[b][0]);
    		pushup(b);
    		return b;
    	}
    }

分块

把序列分为$\sqrt{n}$个块，每个块有$\sqrt{n}$个元素，进行区间操作时整体操作整块，暴力修改散点，时间复杂度$O(n\sqrt n)$。

例题：洛谷P3372 【模板】线段树 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
#include<bits/stdc++.h>
using namespace std;

const int N=1e5+5;
typedef long long ll;
int n,m;
int belong[N];
int block;
ll a[N];
ll sum[500];
ll lazy[500];

void add(int l,int r,ll x){
    int bl=(l-1)/block+1,br=(r-1)/block+1;
    if(bl==br){
        for(int i=l;i<=r;i++){
            a[i]+=x;
        }
        sum[bl]+=(r-l+1)*x;
        return;
    }
    else{
        while(belong[l]==bl){
            a[l]+=x;
            sum[bl]+=x;
            l++;
        }
        while(belong[r]==br){
            a[r]+=x;
            sum[br]+=x;
            r--;
        }
        for(int i=bl+1;i<br;i++){
            lazy[i]+=x;
        }
    }
}

ll query(int l,int r){
    int bl=(l-1)/block+1,br=(r-1)/block+1;
    ll res=0;
    if(bl==br){
        for(int i=l;i<=r;i++){
            res+=a[i];
        }
        res+=(r-l+1)*lazy[bl];
        return res;
    }
    else{
        while(belong[l]==bl){
            res+=a[l]+lazy[bl];
            l++;
        }
        while(belong[r]==br){
            res+=a[r]+lazy[br];
            r--;
        }
        for(int i=bl+1;i<br;i++){
            res+=lazy[i]*block+sum[i];
        }
        return res;
    }
}

int main(){
    cin >> n >> m;
    block=sqrt(n);
    for(int i=1;i<=n;i++){
        cin >> a[i];
        belong[i]=(i-1)/block+1;
        sum[belong[i]]+=a[i];
    }
    for(int i=1;i<=m;i++){
        int opt;
        cin >> opt;
        if(opt==1){
            int l,r;
            ll x;
            cin >> l >> r >> x;
            add(l,r,x);
        }
        else{
            int l,r;
            cin >> l >> r;
            cout << query(l,r) << endl;
        }
    }
    return 0;
}
许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。

快来参与讨论吧~