无向图的双连通分量
边双连通分量(e-DCC)
桥:若被删去,则其相连的两个部分不连通
边双连通分量:极大的不包含桥的连通块
如何找到桥
若dfn[x]<low[y],则边(x,y)是桥(即y无论如何都走不到x)
如何找所有边的双连通分量
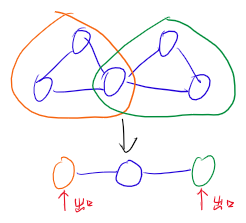
方法一:将所有桥删掉,则剩余的每个连通块就是一个边双连通分量。
方法二:类似有向图的强连通分量,使用一个stack,若搜索完一个点的所有邻接点后dfn[x]=low[x],则这个点与其父节点构成的边为一个桥。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| void tarjan(int u,int from){
dfn[u]=low[u]=++timestamp;
s.push(u);
for(int i=h[u];~i;i=ne[i]){
int j=to[i];
if(!dfn[j]){
tarjan(j,i);
low[u]=min(low[u],low[j]);
if(dfn[u]<low[j]){
is_bridge[i]=is_bridge[i^1];
}
}
else if(i!=(from^1)){
low[u]=min(low[u],dfn[j]);
}
}
if(dfn[u]==low[u]){
++dcc_cnt;
int k;
do{
k=s.top();
s.pop();
id[k]=dcc_cnt;
dcc[dcc_cnt].push_back(k);
}while(k!=u);
}
}
|
模板题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| #include<bits/stdc++.h>
using namespace std;
const int N=5e5+5,M=4e6+5;
int n,m;
int h[N],ne[M],to[M],idx;
int dfn[N],low[N],timestamp;
stack<int>s;
int id[N],dcc_cnt;
vector<int>dcc[N];
bool is_bridge[M];
void add(int a,int b){
to[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void tarjan(int u,int from){
dfn[u]=low[u]=++timestamp;
s.push(u);
for(int i=h[u];~i;i=ne[i]){
int j=to[i];
if(!dfn[j]){
tarjan(j,i);
low[u]=min(low[u],low[j]);
if(dfn[u]<low[j]){
is_bridge[i]=is_bridge[i^1];
}
}
else if(i!=(from^1)){
low[u]=min(low[u],dfn[j]);
}
}
if(dfn[u]==low[u]){
++dcc_cnt;
int k;
do{
k=s.top();
s.pop();
id[k]=dcc_cnt;
dcc[dcc_cnt].push_back(k);
}while(k!=u);
}
}
int main(){
cin >> n >> m;
memset(h,-1,sizeof h);
for(int i=1;i<=m;i++){
int a,b;
cin >> a >> b;
add(a,b),add(b,a);
}
for(int i=1;i<=n;i++){
if(!dfn[i])tarjan(i,-1);
}
cout << dcc_cnt << endl;
for(int i=1;i<=dcc_cnt;i++){
cout << dcc[i].size() << ' ';
for(auto x:dcc[i]){
cout << x << ' ';
}
cout << endl;
}
return 0;
}
|
点双连通分量(v-DCC)
割点:若被删去,则其相连的两部分不连通
点双连通分量:极大的不包含割点的连通块
每个割点都至少属于两个点双连通分量
如何求割点
low[y]$\ge$dfn[x](y搜不到x上面)
(1)若$x$不是根节点,则$x$是割点
(2)若$x$是根节点,则若还有至少一个$y_i$满足low[$y_i$]$\ge$dfn[x],则$x$是割点
如何求点双连通分量
stack,若low[y]$\ge$dfn[x] ,则子树个数$cnt$++,若$x$不是根节点或还有至少一个$y_i$满足low[$y_i$]$\ge$dfn[x],即cnt>1,则$x$为割点,将栈中元素弹出直至$y$为止,这些点和$x$都属于这个点双连通分量
模板题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
| #include<bits/stdc++.h>
using namespace std;
const int N=5e5+5,M=4e6+5;
int n,m;
int h[N],to[M],ne[M],idx;
int dfn[N],low[N],timestamp;
stack<int>s;
int dcc_cnt;
vector<int>dcc[N];
int root;
void add(int a,int b){
to[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void tarjan(int u){
dfn[u]=low[u]=++timestamp;
s.push(u);
if(u==root&&h[u]==-1){
dcc_cnt++;
dcc[dcc_cnt].push_back(u);
s.pop();
return;
}
int cnt=0;
for(int i=h[u];~i;i=ne[i]){
int j=to[i];
if(!dfn[j]){
tarjan(j);
low[u]=min(low[u],low[j]);
if(dfn[u]<=low[j]){
cnt++;
++dcc_cnt;
int y;
do{
y=s.top();
s.pop();
dcc[dcc_cnt].push_back(y);
}while(y!=j);
dcc[dcc_cnt].push_back(u);
}
}
else{
low[u]=min(low[u],dfn[j]);
}
}
}
int main(){
memset(h,-1,sizeof h);
cin >> n >> m;
for(int i=1;i<=m;i++){
int a,b;
cin >> a >> b;
if(a!=b)add(a,b),add(b,a);
}
for(root=1;root<=n;root++){
if(!dfn[root]){
tarjan(root);
}
}
cout << dcc_cnt << endl;
for(int i=1;i<=dcc_cnt;i++){
cout << dcc[i].size() << ' ';
for(auto x:dcc[i]){
cout << x << ' ';
}
cout << endl;
}
return 0;
}
|
例题:洛谷P3225 [HNOI2012] 矿场搭建
题目大意:给定一个无向图,问最少在几个点上设置出口,可以使得不管哪个点坍塌,其余所有点都可以与某个出口连通,并求出方案数。
分析:
首先不难发现,如果只有一个出口的话,那么如果这个出口坍塌,则其余点一定无法与出口连通,因此,至少有两个出口。
可以把整个无向图分成若干个连通块,对于每个连通块单独求出答案。
若当前连通块中没有割点,则直接设置两个出口即可,方案数为$C_{size}^{2}=\frac{size \times (size-1)}{2}$。
若当前连通块中有割点,则可以进行缩点,将所有割点建一个新点,点双连通分量中除了割点外的其他点建一个点,并连向点双连通分量中的割点,形成一个新图,则可以发现,只需在所有度数为1的点,即这个对应的连通块除了割点以外的任意点上建立一个出口就能保证所有点可以和出口连通,方案数为$size-1$。
不难发现,缩点后点的度数就等于点双连通分量中割点个数。
注意特判连通块只有一个点的情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
| #include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ll;
const int N=1e3+5,M=1e3+5;
int n,m;
int h[N],to[M],ne[M],idx;
int dfn[N],low[N],timestamp;
stack<int>s;
int dcc_cnt;
vector<int>dcc[N];
bool cut[N];
int root;
void add(int a,int b){
to[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void tarjan(int u){
dfn[u]=low[u]=++timestamp;
s.push(u);
if(u==root&&h[u]==-1){
dcc_cnt++;
dcc[dcc_cnt].push_back(u);
s.pop();
return;
}
int cnt=0;
for(int i=h[u];~i;i=ne[i]){
int j=to[i];
if(!dfn[j]){
tarjan(j);
low[u]=min(low[u],low[j]);
if(dfn[u]<=low[j]){
cnt++;
if(u!=root||cnt>1)cut[u]=true;
++dcc_cnt;
int y;
do{
y=s.top();
s.pop();
dcc[dcc_cnt].push_back(y);
}while(y!=j);
dcc[dcc_cnt].push_back(u);
}
}
else{
low[u]=min(low[u],dfn[j]);
}
}
}
int main(){
int T=1;
while(cin >> m,m){
while(!s.empty())s.pop();
for(int i=1;i<=dcc_cnt;i++){
dcc[i].clear();
}
idx=n=timestamp=dcc_cnt=0;
memset(h,-1,sizeof h);
memset(dfn,0,sizeof dfn);
memset(cut,0,sizeof cut);
for(int i=1;i<=m;i++){
int a,b;
cin >> a >> b;
n=max(n,max(a,b));
add(a,b),add(b,a);
}
for(root=1;root<=n;root++){
if(!dfn[root]){
tarjan(root);
}
}
int res=0;
ll num=1;
for(int i=1;i<=dcc_cnt;i++){
int cnt=0;
for(int j=0;j<dcc[i].size();j++){
if(cut[dcc[i][j]])cnt++;
}
if(cnt==0){
if(dcc[i].size()>1)res+=2,num*=dcc[i].size()*(dcc[i].size()-1)/2;
else res++;
}
else if(cnt==1){
res++,num*=dcc[i].size()-1;
}
}
cout << "Case " << T++ << ": " << res << ' ' << num << endl;
}
return 0;
}
|