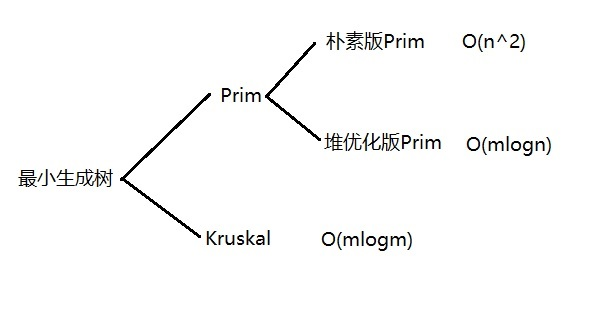
最小生成树

Prim
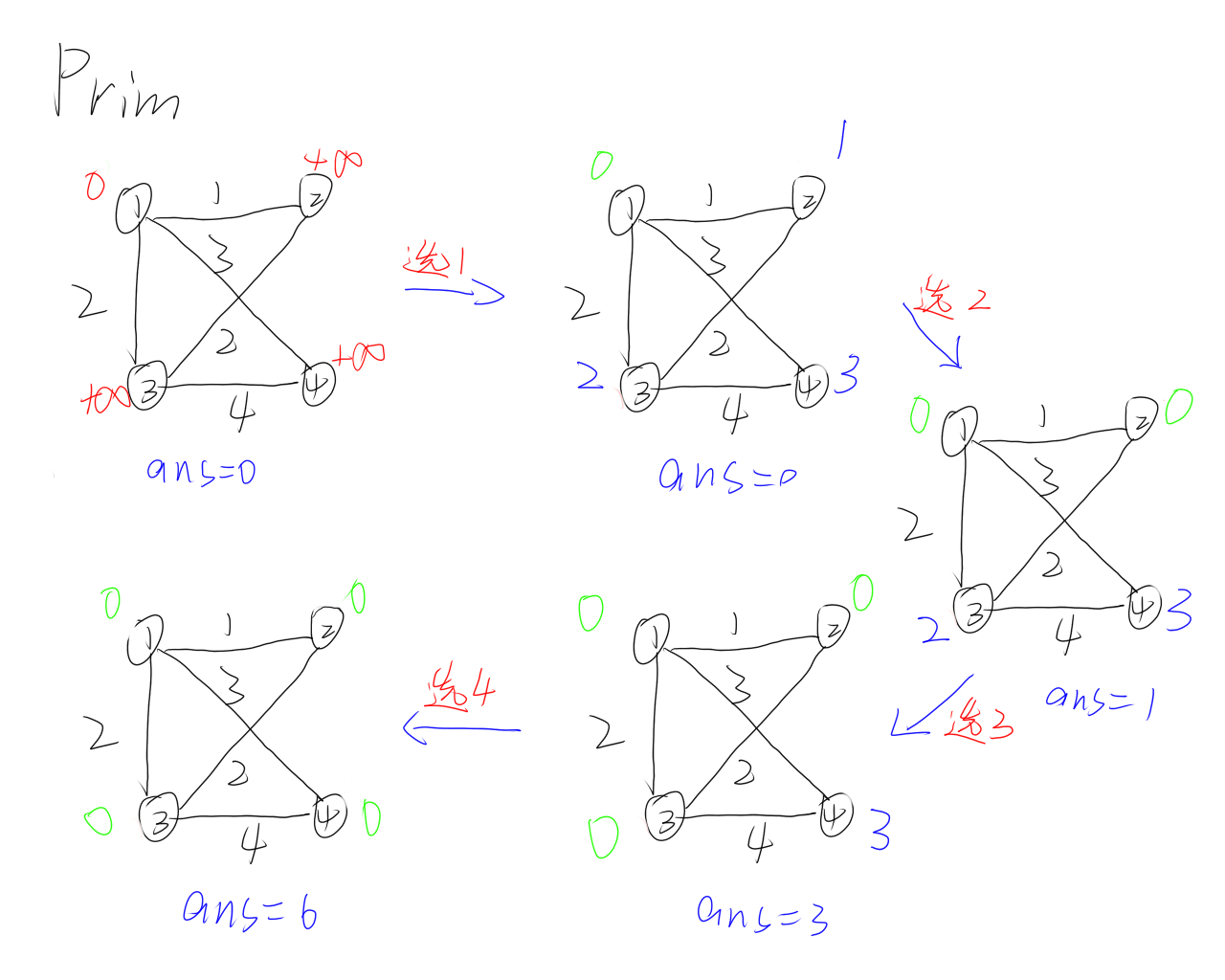
朴素版Prim
稠密图
存储:邻接矩阵
做法:
- 初始化距离
- 循环$n$次,每次找到距离集合最近的点,加入集合,用这个点更新其他点到集合的距离

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| #include<bits/stdc++.h>
using namespace std;
const int N=505;
int n,m;
int g[N][N];
int d[N];
bool st[N];
int prim(){
memset(d,0x3f,sizeof d);
int len=0;
d[1]=0;
for(int i=1;i<=n;i++){
int u=-1;
for(int j=1;j<=n;j++){
if(!st[j]&&(d[u]>d[j]||u==-1))u=j;
}
if(d[u]==0x3f3f3f3f)return 0x3f3f3f3f;
len+=d[u];
st[u]=1;
d[u]=0;
for(int j=1;j<=n;j++){
d[j]=min(d[j],d[u]+g[u][j]);
}
}
return len;
}
int main(){
memset(g,0x3f,sizeof g);
cin >> n >> m;
for(int i=1;i<=m;i++){
int u,v,w;
cin >> u >> v >> w;
g[u][v]=g[v][u]=min(g[u][v],w);
}
for(int i=1;i<=n;i++){
g[i][i]=0;
}
int ans=prim();
if(ans==0x3f3f3f3f)cout << "impossible";
else cout << ans;
return 0;
}
|
堆优化Prim
类似$Dijkstra$的堆优化,不常用,可用$Kruskal$替代
Kruskal
稀疏图
存储:结构体
做法:
- 排序所有边
- 每次选择最短的边,若这条边的两点不在同一集合(并查集),则加入这条边,直到所有的点都在同一集合内
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| #include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,M=2e5+5;
struct Edge{
int u,v,w;
Edge():u(),v(),w(){}
Edge(int a,int b,int c):u(a),v(b),w(c){}
bool operator<(const Edge &a)const{
return w<a.w;
}
}edge[M];
int n,m;
int fa[N];
int find(int x){
return fa[x]==x?x:fa[x]=find(fa[x]);
}
void merge(int x,int y){
x=find(x),y=find(y);
fa[x]=y;
}
int idx;
int kruskal(){
int len=0;
for(int i=1;i<=m;i++){
auto t=edge[i];
if(find(t.u)!=find(t.v)){
merge(t.u,t.v);
idx++;
len+=t.w;
if(idx==n-1)return len;
}
}
return 0x3f3f3f3f;
}
int main(){
cin >> n >> m;
for(int i=1;i<=n;i++){
fa[i]=i;
}
for(int i=1;i<=m;i++){
int u,v,w;
cin >> u >> v >> w;
edge[i]={u,v,w};
}
sort(edge+1,edge+m+1);
int ans=kruskal();
if(ans==0x3f3f3f3f)cout << "impossible";
else cout << ans;
return 0;
}
|