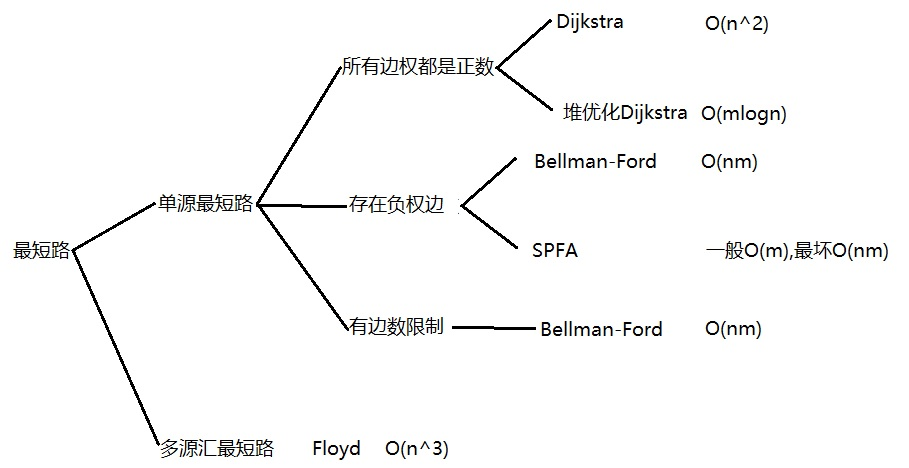
最短路
单源最短路 一个点到其他所有点的长度
Dijkstra 稠密图
存储:邻接矩阵
做法:
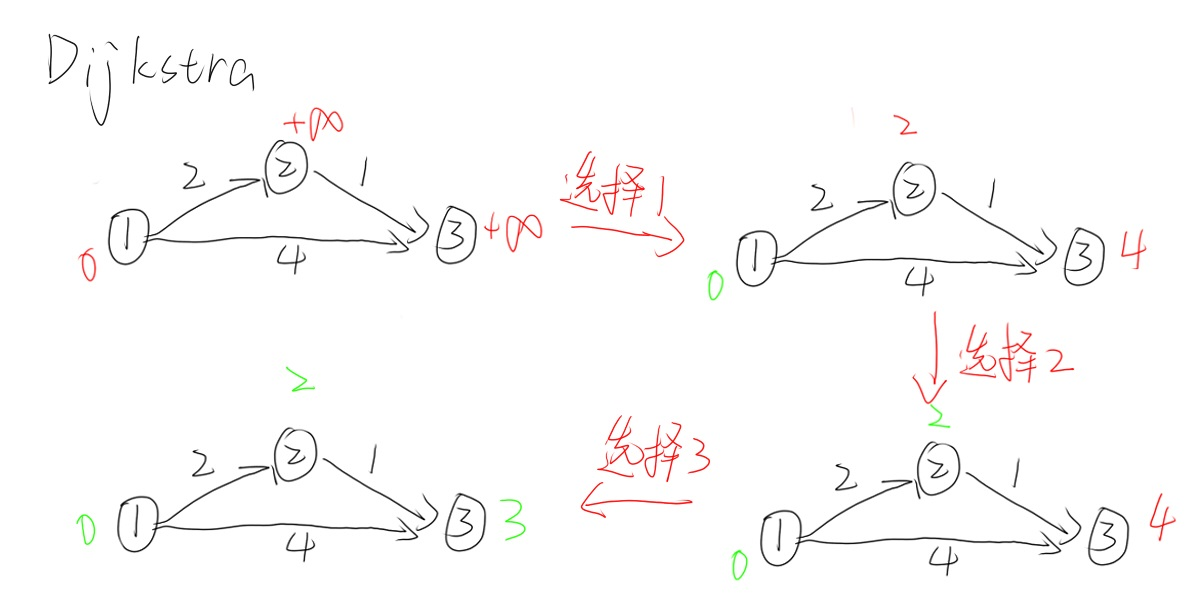
初始化:$dis[1]=0,dis[i]=+\infty$
循环$n$次,每次选取没有被确定的距离最近的点$t$,则$t$的值被确定,用$t$更新其他未被确定的点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 #include <bits/stdc++.h> using namespace std;const int N=505 ;int n,m;int g[N][N];int d[N];bool vis[N];int dijkstra () memset (d,0x3f ,sizeof d); d[1 ]=0 ; for (int i=1 ;i<=n;i++){ int t=0 ; for (int j=1 ;j<=n;j++){ if (d[j]<d[t]&&vis[j]==0 )t=j; } vis[t]=1 ; for (int j=1 ;j<=n;j++){ if (vis[j]==0 ){ d[j]=min (d[j],d[t]+g[t][j]); } } } if (d[n]==0x3f3f3f3f )return -1 ; return d[n]; } int main () memset (g,0x3f ,sizeof g); cin >> n >> m; for (int i=1 ;i<=m;i++){ int u,v,w; cin >> u >> v >> w; g[u][v]=min (g[u][v],w); } cout << dijkstra (); return 0 ; }
堆优化Dijkstra 稀疏图
存储:邻接表
做法:
初始化:$dis[1]=0,dis[i]=+\infty$,将${0,1}$插入优先队列。
重复至队列为空:取出队首元素,若当前点已被确定,则进行下一次循环,否则当前点确定,用当前点更新其他点,若有点$v$被更新,则将${d[v],v}$插入队列。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 #include <bits/stdc++.h> using namespace std;const int N=2e5 +5 ;int n,m;int h[N],ne[N],to[N],e[N];int cnt;void addedge (int u,int v,int w) ne[++cnt]=h[u]; to[cnt]=v; e[cnt]=w; h[u]=cnt; } int d[N];bool vis[N];int dijkstra () priority_queue<pair<int ,int >,vector<pair<int ,int >>,greater<pair<int ,int >>>q; memset (d,0x3f ,sizeof d); d[1 ]=0 ; q.push ({0 ,1 }); while (!q.empty ()){ auto t=q.top (); q.pop (); int u=t.second; if (vis[u])continue ; vis[u]=1 ; for (int i=h[u];i;i=ne[i]){ if (d[to[i]]>d[u]+e[i]){ d[to[i]]=d[u]+e[i]; q.push ({d[to[i]],to[i]}); } } } if (d[n]==0x3f3f3f3f )return -1 ; return d[n]; } int main () cin >> n >> m; for (int i=1 ;i<=m;i++){ int u,v,w; cin >> u >> v >> w; addedge (u,v,w); } cout << dijkstra (); return 0 ; }
Bellman-Ford 存边:结构体
做法:
循环$n$次,每次先备份数组,再通过备份遍历所有边,更新所有点
若限制走$k$条边,则循环$k$次
注意:
更新时$d[v]=min(d[v],backup[u]+w)$
负权边可能会把$d[n]$更新,但到不了第$n$个点,所以不能判断$d[n]==inf$,而是大于一个较大的数
应用:求$1$到$n$经过最多$k$条边的最短长度
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 #include <bits/stdc++.h> using namespace std;const int N=505 ,M=1e4 +5 ;int n,m,k;struct edge { int u,v,w; edge ():u (),v (),w (){} edge (int a,int b,int c):u (a),v (b),w (c){} }e[M]; int d[N];int bellman_ford () memset (d,0x3f ,sizeof d); d[1 ]=0 ; for (int i=1 ;i<=k;i++){ int backup[N]; memcpy (backup,d,sizeof d); for (int j=1 ;j<=m;j++){ auto t=e[j]; int u=t.u,v=t.v,w=t.w; d[v]=min (d[v],backup[u]+w); } } if (d[n]>=5000000 )return -1e9 ; return d[n]; } int main () cin >> n >> m >> k; for (int i=1 ;i<=m;i++){ int u,v,w; cin >> u >> v >> w; e[i]={u,v,w}; } int ans=bellman_ford (); if (ans==-1e9 )cout << "impossible" ; else cout << ans; return 0 ; }
SPFA 稀疏图
存边:邻接表
考虑Bellman-Ford 的优化
每次更新边时只有当前节点的$dist$变小了,从当前点出发的边才会更新其他边,所以每次记录变小的点,更新变小的点所连的边
做法:
把$1$入队
循环直到队列为空:取出队首,更新以当前点为起点的边,若某个点被修改,且这个点不在队列里,将这个点入队
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 #include <bits/stdc++.h> using namespace std;const int N=1e5 +5 ;int n,m;int h[N],ne[N],to[N],e[N];int cnt;void addedge (int u,int v,int w) ne[++cnt]=h[u]; to[cnt]=v; e[cnt]=w; h[u]=cnt; } int d[N];bool inq[N];int spfa () queue<int >q; memset (d,0x3f ,sizeof d); d[1 ]=0 ; q.push (1 ); inq[1 ]=1 ; while (!q.empty ()){ int u=q.front (); q.pop (); inq[u]=0 ; for (int i=h[u];i;i=ne[i]){ if (d[to[i]]>d[u]+e[i]){ d[to[i]]=d[u]+e[i]; if (!inq[to[i]]){ q.push (to[i]); inq[to[i]]=1 ; } } } } return d[n]; } int main () cin >> n >> m; for (int i=1 ;i<=m;i++){ int u,v,w; cin >> u >> v >> w; addedge (u,v,w); } int ans=spfa (); if (ans==0x3f3f3f3f )cout << "impossible" ; else cout << ans; return 0 ; }
判断负环 原理:若最短路经过了$\ge n$条边,则必定有一个点走过了两次及以上,则一定存在负环
做法:用$idx$数组记录当前最短路走过的边数,当当前点的$idx$大于等于$n$时则存在负环
因为不需要求具体数值,所以可以不初始化
因为图可能不连通,所以刚开始要全部入队
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 #include <bits/stdc++.h> using namespace std;const int N=2e5 +5 ;int n,m;int h[N],ne[N],to[N],e[N];int cnt;void addedge (int u,int v,int w) ne[++cnt]=h[u]; to[cnt]=v; e[cnt]=w; h[u]=cnt; } int d[N];bool inq[N];int idx[N];bool spfa () queue<int >q; for (int i=1 ;i<=n;i++){ q.push (i); inq[i]=1 ; } while (!q.empty ()){ int u=q.front (); q.pop (); inq[u]=0 ; for (int i=h[u];i;i=ne[i]){ if (d[to[i]]>d[u]+e[i]){ d[to[i]]=d[u]+e[i]; idx[to[i]]=idx[u]+1 ; if (idx[to[i]]>n)return 1 ; if (!inq[to[i]]){ q.push (to[i]); inq[to[i]]=1 ; } } } } return 0 ; } int main () cin >> n >> m; for (int i=1 ;i<=n;i++){ addedge (0 ,i,0 ); } for (int i=1 ;i<=m;i++){ int u,v,w; cin >> u >> v >> w; addedge (u,v,w); } if (spfa ())cout << "Yes" ; else cout << "No" ; return 0 ; }
差分约束 应用:求不等式组的可行解,其中每个不等式形如 $x_i \le x_j+c_k$
思路:
根据最短路的三角不等式,点$j$ 向点 $i$ 连一条长度为 $c$ 的边,那么如果 $dist_i>dist_j+c$ ,则 $dist_i$ 会被更新为 $dist_j+c$ ,因此最短路算法结束后,一定有 $dist_i \le dist_j+c$。
因此,可以把不等式 $x_i \le x_j+c_k$ 看做一条 $x_j$ 到 $x_i$ 长度为 $x_k$ 的一条边 ,这样可以把原不等式组转化为图论问题。
由于需要满足所有的不等式,因此最短路的源点必须满足从这个点出发可以走到所有的边。可以建立一个超级源点,使这个点可以遍历到所有边。
可以发现,建成的图可能存在负环,则容易看出若出现负环,则原不等式组无解。
这样求出来的解是最大解,如果要求最小解,可以转化为求最长路,判断正环即可。
如果出现形如 $x_i \le c$ 的不等式,则建立一个超级源点 $S$ ,则可以转化为 $x_i \le S + c$ ,即建立一个 $S$ 到 $x_i$,长度为 $c$ 的边。
多源汇最短路 任意两点之间的长度
Floyd 存储:邻接矩阵
做法:初始化,枚举中间节点,起点,终点,更新
注意:负权边可能会把$d[n]$更新,但到不了第$n$个点,所以不能判断$d[n]==inf$,而是大于一个较大的数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 #include <bits/stdc++.h> using namespace std;const int N=205 ;int n,m,q;int g[N][N];void floyd () for (int k=1 ;k<=n;k++){ for (int i=1 ;i<=n;i++){ for (int j=1 ;j<=n;j++){ g[i][j]=min (g[i][j],g[i][k]+g[k][j]); } } } } int main () memset (g,0x3f ,sizeof g); cin >> n >> m >> q; for (int i=1 ;i<=m;i++){ int u,v,w; cin >> u >> v >> w; g[u][v]=min (g[u][v],w); } for (int i=1 ;i<=n;i++){ g[i][i]=0 ; } floyd (); for (int i=1 ;i<=q;i++){ int u,v; cin >> u >> v; if (g[u][v]>1e9 )cout << "impossible\n" ; else cout << g[u][v] << endl; } return 0 ; }