有向图的强连通分量
一个强连通分量中的点都可以互相到达
作用:有向图$\xRightarrow{缩点}$ 有向无环图(DAG)
Tarjan算法求强连通分量(SCC)

那么如何判断一个点是否在一个SCC中?
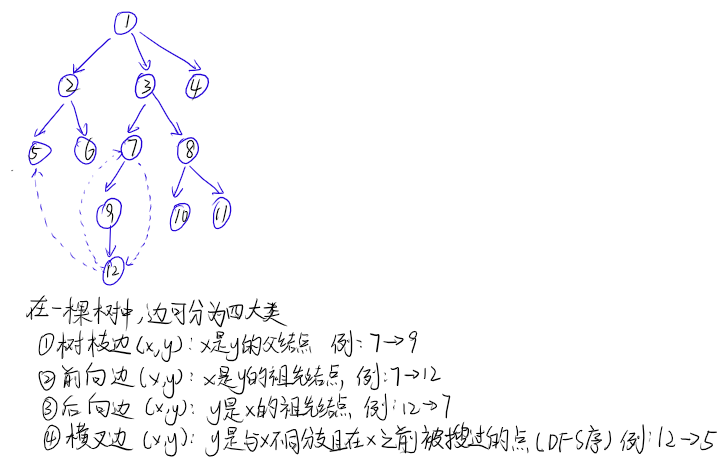
情况1:存在一条后向边指向祖先节点
情况2:先走过横插边,后走到祖先节点
若按照dfs搜索的顺序给每个点一个编号,可以发现:
- 若当前边为树枝边或前向边,则y>x
- 若当前边为后向边或横叉边,则y<x
因此,对于每个点定义两个时间戳:
dfn[u]表示遍历到$u$的时间戳low[u]表示从$u$开始走,所能遍历到的最小时间戳
若存在一个点$u$,dfn[u]=low[u],则$u$是其所在强连通分量的最高点
由此可以得到Tarjan算法:
顺序遍历每个节点,若没被遍历过,则进行搜索。首先记录当前点的时间戳并将这个点入栈,然后枚举每条边。
- 若这条边的终点没有被遍历过,则遍历终点,更新当前点的low(由于终点是可以被当前点遍历到的,因此当前点的low就等于两个点low的最小值。
- 若终点被遍历过,但终点仍然在栈里,则表示这条边是一个横插边,因此可以用终点的dfn更新当前点的low
枚举完所有边后,若当前点的low=dfn,则表示当前点是其所处强连通分量的最高点,因此从栈顶一直到当前点均为这个强连通分量的点,记录即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| void tarjan(int u){
dfn[u]=low[u]=++timestamp;
stk[++top]=u,in_stk[u]=true;
for(int i=h[u];i;i=ne[i]){
int j=to[i];
if(!dfn[j]){
tarjan(j);
low[u]=min(low[u],low[j]);
}
else if(in_stk[j]){
low[u]=min(low[u],dfn[j]);
}
}
if(dfn[u]==low[u]){
int y;
++scc_cnt;
do{
y=stk[top--];
in_stk[y]=false;
id[y]=scc_cnt;
}while(y!=u);
}
}
|
时间复杂度$O(n+m)$
连通分量递减的顺序一定是拓扑序
求完强连通分量后,即可进行缩点,将原图转化为一个拓扑图:
1
2
3
4
5
6
7
| for(int i=1;i<=n;i++){
for(int j=h[i];j;j=ne[j]){
if(id[i]!=id[to[j]]){
addedge(id[i],id[to[j]]);
}
}
}
|
模板题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
| #include<bits/stdc++.h>
using namespace std;
const int N=5e5+5,M=4e6+5;
int n,m;
int h[N],ne[M],to[M],idx;
int id[N],scc_cnt,timestamp;
vector<int>scc[N];
int dfn[N],low[N];
stack<int>s;
bool in_stk[N];
void addedge(int u,int v){
ne[++idx]=h[u];
h[u]=idx;
to[idx]=v;
}
void tarjan(int u){
dfn[u]=low[u]=++timestamp;
s.push(u),in_stk[u]=true;
for(int i=h[u];i;i=ne[i]){
if(!dfn[to[i]]){
tarjan(to[i]);
low[u]=min(low[u],low[to[i]]);
}
else if(in_stk[to[i]]){
low[u]=min(low[u],dfn[to[i]]);
}
}
if(dfn[u]==low[u]){
++scc_cnt;
int k;
do{
k=s.top();
s.pop();
in_stk[k]=false;
id[k]=scc_cnt;
scc[scc_cnt].push_back(k);
}while(k!=u);
}
}
bool out[N];
int main(){
cin >> n >> m;
for(int i=1;i<=m;i++){
int u,v;
cin >> u >> v;
addedge(u,v);
}
for(int i=1;i<=n;i++){
if(!dfn[i])tarjan(i);
}
cout << scc_cnt << endl;
for(int i=1;i<=n;i++){
int k=id[i];
if(out[k])continue;
out[k]=1;
sort(scc[k].begin(),scc[k].end());
for(auto x:scc[k]){
cout << x << ' ';
}
cout << endl;
}
return 0;
}
|