树与图的搜索
有向图存储:
- 邻接矩阵:$g[a][b]=x$表示从$a$到$b$的一条长度为$x$的边
- 邻接表:在每个节点上开一个单链表表示当前点到链表中的点有一条边
对于无向图,每一条边$(u,v)$可以看作有向图中的$(u,v),(v,u)$两条边
邻接矩阵:
1
2
3
4
| int g[N][N];
void addedge(int u,int v,int w){
g[u][v]=w;
}
|
邻接表:
1
2
3
4
5
6
7
8
| int h[N],ne[N],to[N],e[N];
int cnt;
void addedge(int u,int v,int w){
ne[++cnt]=h[u];
to[cnt]=v;
e[cnt]=w;
h[u]=cnt;
}
|
树的搜索:

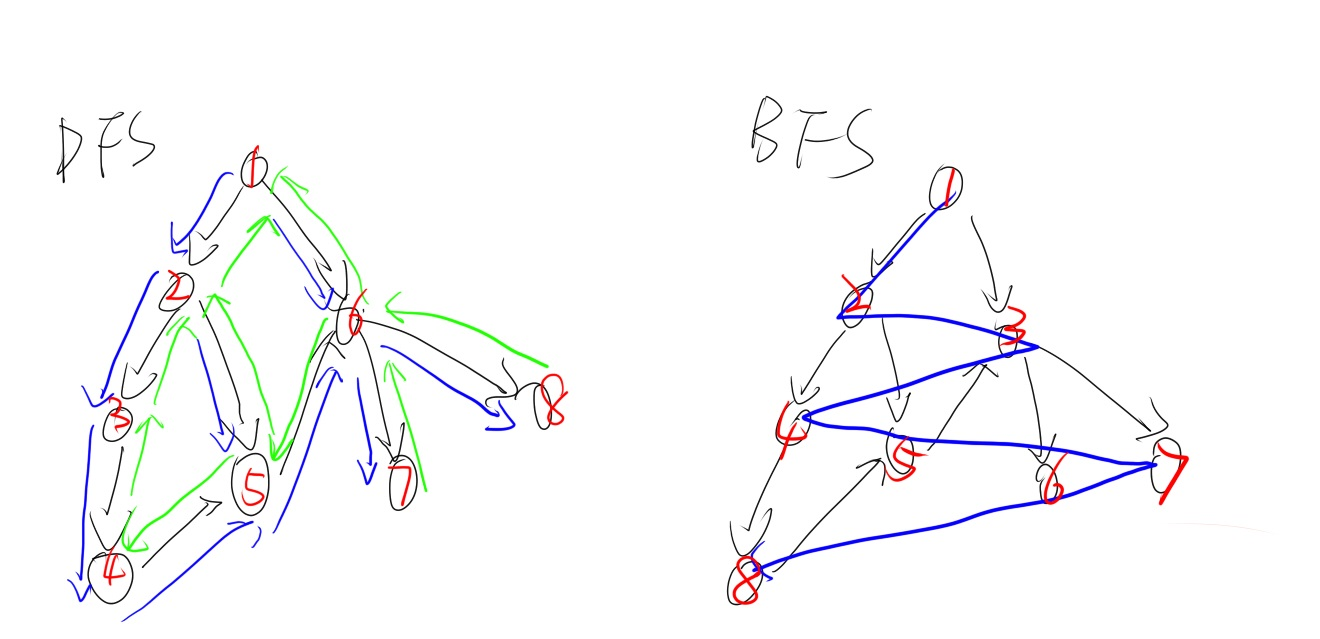
深度优先搜索
以邻接表存图为例:
1
2
3
4
5
6
7
| int st[N];
void dfs(int u){
st[u]=true;
for(int i=h[u];i;i=ne[i]){
if(!st[to[i]])dfs(to[i]);
}
}
|
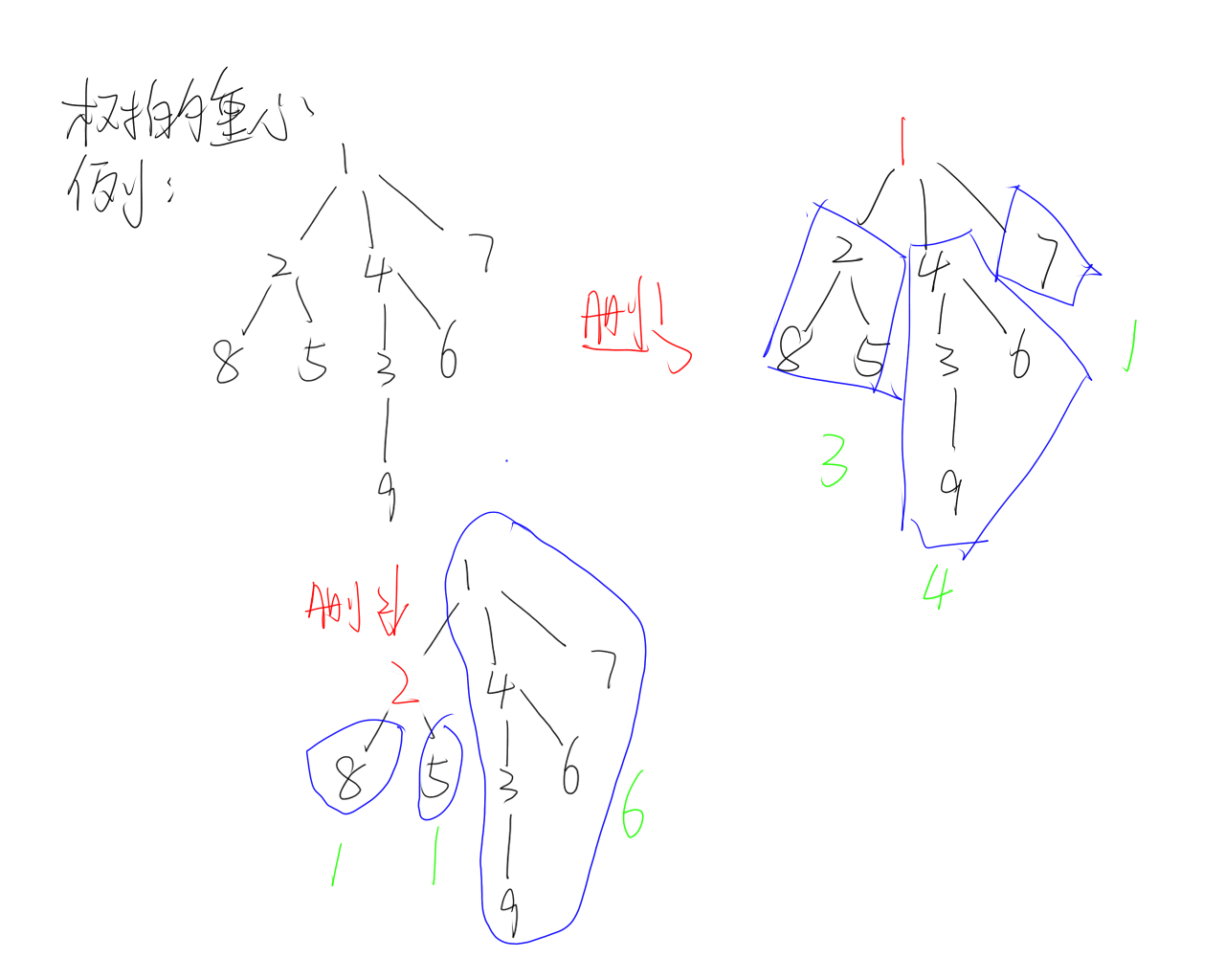
应用:求子树的大小
例:
树的重心:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。
输入一个$n$,表示节点个数,输入$n-1$条边,求树的重心
分析:可以发现删除点后连通块的大小就等于这个点所有的子树大小和所有点减去这棵树及其子树大小的最大值($max(sz[v],n-sz[u])$)

因此在遍历时求出所有子树大小,每次遍历完子树时求出每个点删除后的最大连通块大小即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| #include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,ans=1e9;
int h[N],ne[N*2],to[N*2];
int cnt;
void addedge(int u,int v){
ne[++cnt]=h[u];
to[cnt]=v;
h[u]=cnt;
}
int sz[N];
bool st[N];
void dfs(int u){
int mx=0;
st[u]=1;
sz[u]=1;
for(int i=h[u];i;i=ne[i]){
if(!st[to[i]]){
dfs(to[i]);
sz[u]+=sz[to[i]];
mx=max(mx,sz[to[i]]);
}
}
mx=max(mx,n-sz[u]);
ans=min(ans,mx);
}
int main(){
cin >> n;
for(int i=1;i<n;i++){
int u,v;
cin >> u >> v;
addedge(u,v);
addedge(v,u);
}
dfs(1);
cout << ans;
return 0;
}
|
广度优先搜索
例:给定点数$n$,$m$条边,求$1$到$n$的距离
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| #include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,m;
int h[N],ne[N*2],to[N*2];
int cnt;
void addedge(int u,int v){
ne[++cnt]=h[u];
to[cnt]=v;
h[u]=cnt;
}
int d[N];
void bfs(){
queue<int>q;
q.push(1);
memset(d,-1,sizeof d);
d[1]=0;
while(!q.empty()){
int t=q.front();
q.pop();
for(int i=h[t];i;i=ne[i]){
if(d[to[i]]==-1){
d[to[i]]=d[t]+1;
q.push(to[i]);
}
}
}
}
int main(){
cin >> n >> m;
for(int i=1;i<=m;i++){
int u,v;
cin >> u >> v;
addedge(u,v);
}
bfs();
cout << d[n];
return 0;
}
|