置换群
置换群
置换:把 $1,2,\cdots,n$ 映射到一个 1 到 n 的排列 $p_1,p_2,\cdots,p_n$ 称为置换,可记为 $f(x)=p_x$
循环置换:即把 $1,2,\cdots,n-1,n$ 映射到 $2,3,\cdots,n,1$
置换的乘积:即复合函数,如有两个置换为 $f(x),g(x)$,则这两个置换的乘积为 $g(f(x))$
性质:任意一个置换都可以拆成若干个循环置换的乘积
置换群:$1\sim n$ 的置换共有 $n!$ 种,这 $n!$ 种置换称为一个置换群,且置换群的子集也是置换群
Burnside 引理和 Polya 定理
求在 $n$ 个点的环上染色,共 $m$ 种颜色的方案数
Burnside引理:对于每个置换不动点个数的平均值就是不同的方案数
不动点:对于某种方案,经过置换之后若某个的的方案不变,则这个点称为这个置换的不动点。
Polya定理:将一个置换拆解成多个循环置换,共 $c$ 种颜色,由于每个循环内的颜色一定一样,每个循环之间相互独立,设循环数 $k$ ,则循环的不动点数为 $c^k$
使用 Polya 定理,必须保证循环之间相互独立。
例题1:AcWing 3133. 串珠子(Polya 定理)
给定 $ M $ 种不同颜色的珠子,每种颜色的珠子的个数都足够多。
现在要从中挑选 $ N $ 个珠子,串成一个环形手链。
请问一共可以制作出多少种不同的手链。
注意,如果两个手链经旋转或翻转后能够完全重合在一起,对应位置的珠子颜色完全相同,则视为同一种手链。
输入格式
输入包含多组测试数据。
每组测试数据占一行,包含两个整数 $ M,N $。
最后一行包含
0 0表示输入结束。输出格式
每组数据输出一个占一行的整数表示结果。
数据范围
$ N,M > 0 $,
$ N \times M \le 32 $输入样例:
2
3
4
5
6
7
8
2 1
2 2
5 1
2 5
2 6
6 2
0 0输出样例:
2
3
4
5
6
7
2
3
5
8
13
21样例解释
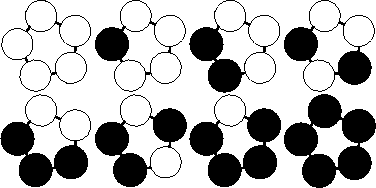
当 $ M=2,N=5 $ 时,一共可以制作出 $ 8 $ 种不同的手链,如下图。
分析:
一共两种操作:旋转和翻转。
先考虑旋转,可以旋转 $k=0,1,\cdots,n-1$ 次
对于每种方案 ,则找到循环等价于找到一个 $t$ ,满足 $x+kt\equiv x \pmod n$,即 $kt \equiv 0 \pmod n \Longleftrightarrow kt+nr=0$,其最小解为 $t=\frac n d,d=(n,k)$。因此,每个循环的点数为 $\frac n d$ ,所以循环数就是 $d=(n,k)$,则不动点的个数就是 $m^d$,所以总不动点个数就是 $\sum_{k=0}^{n-1}m^{(n,i)}$
再考虑翻转:
若 $n$ 为奇数,则对称轴共 $n$ 个,每个对称轴对应一组方案,其循环为对称点相互配对,对称轴穿过的点单独一个循环,共 $\frac{n+1} 2$ 个,因此不动点个数为 $n\cdot m^{\frac{n+1}2}$
若 $n$ 为偶数,则对称轴分为两类:
若对称轴穿过两个点,则这两个点各自一个循环,其余点两两配对,共 $\frac n 2 +1$ 个循环,有 $\frac n 2$ 个这种对称轴,因此不动点个数为 $\frac n 2\cdot m ^{\frac n 2 +1} $
若对称轴在两点之间,共 $\frac n 2 $ 个对称轴,点两两配对,共 $\frac n 2$ 个循环,因此不动点个数为 $\frac n 2 \cdot m^{\frac n 2}$
所以 $n$ 为偶数时,不动点个数为 $\frac n 2\cdot m ^{\frac n 2 +1}+\frac n 2 \cdot m^{\frac n 2} $
由于一共有 $2n$ 种置换,因此将不动点个数相加除以 $2n$ 即为答案
1 |
|
第一个 for 循环可以使用欧拉定理+莫比乌斯反演优化
给定 $ m $ 种不同颜色的魔法珠子,每种颜色的珠子的个数都足够多。
现在要从中挑选 $ n $ 个珠子,串成一个环形魔法手链。
魔法珠子之间存在 $ k $ 对排斥关系,互相排斥的两种颜色的珠子不能相邻,否则会发生爆炸。(同一种颜色的珠子之间也可能存在排斥)
请问一共可以制作出多少种不同的手链。
注意,如果两个手链经旋转后能够完全重合在一起,对应位置的珠子颜色完全相同,则视为同一种手链。
答案对 $ 9973 $ 取模。
输入格式
第一行包含整数 $ T $,表示共有 $ T $ 组测试数据。
每组数据第一行包含三个整数 $ n,m,k $。
接下来 $ k $ 行,每行包含两个整数 $ a,b $,表示颜色 $ a $ 的珠子不能和颜色 $ b $ 的珠子相邻。
$ m $ 种颜色编号为 $ 1 \sim m $。
输出格式
每组数据输出一行一个整数,表示答案。
数据范围
$ 1 \le T \le 10 $,
$ 1 \le n \le 10^9 $,
$ gcd(n, 9973) = 1 $,
$ 1 \le m \le 10 $,
$ 0 \le k \le \frac{m(m+1)}{2} $,
$ 1 \le a,b \le m $输入样例:
2
3
4
5
6
7
8
9
10
11
3 2 0
3 2 1
1 2
3 2 2
1 1
1 2
3 2 3
1 1
1 2
2 2输出样例:
2
3
4
2
1
0
分析:
只有一种操作:旋转。
由于环之间有限制,因此不能使用 Polya 定理。
设旋转了 $k=0,1,2,\cdots ,n-1$ 次,设 $d=(n,k)$,则共有 $d$ 个循环,每个循环有 $\frac n d$ 个点(理由同上题)
令 $k’=\frac k d,n’=\frac n d$,由于共 $\frac n d$ 个点,每个点间的间隔为 $d$ ,因此每个点离起点的距离为 $d$ 的倍数,所以可以将 $0,d,2d,\cdots$ 映射为 $0,1,2,\cdots$,则原环变为一个长度为 $n’$ 的环,每次跳 $k’$ 步。由于 $(k’,n’)=1$ ,所以每次走 $k’$ 步一定可以遍历环中的所有点,即 $k’\cdot 0,k’\cdot 1,k’\cdot2 ,\cdots,k’\cdot (n’-1)$ 构成一个模 $n’$ 的简化剩余系(缩系)
由于每一段的起点为 $x,x+1,\cdots,x+d-1$,所以从起点开始每个长度为 $d$ 的段的颜色与上一个长度为 $d$ 的段的颜色一定相同,因此整体的颜色就取决于第一段的颜色,因此求不动点的数量只需关注第一段即可。由于每一段的最后一个点与下一段的第一个点相邻,而下一段的第一个点与这一段的第一个点相同,因此可以看成每一段的最后一个点与第一个点相邻,因此只需关注长度为 $d$ 的环染色方案即可。
接下来可以暴力求出这个环的染色方案数,使用 dp ,$f_{i,j}$ 表示已经染完了 $i$ 个格子,第 $i$ 个点染 $j$ 种颜色的方案数。枚举第一个格子染的颜色,若当前枚举到第 $k$ 种颜色,则初始化 $f_{0,k}=1$,$f_{i,j}=\sum_{k=0}^{m} f_{i-1,k}$,可以使用矩阵乘法优化。
记 $F_i=[f_{i,1},f_{i,2},\cdots,f_{i,m}]$,则 $F_i=F_{i-1}\cdot M$,其中 $M$ 的 $(a_i,b_i)=0$,其余项为 $1$ ($(a_i,b_i)$ 表示一组限制条件)
则 $F_d=F_0\cdot M^d$,使用矩阵快速幂优化。
由于 $n$ 很大,因此枚举步数 $k$ 时不能直接枚举,可以将所有的循环置换分类,由于每个循环置换的方案数只取决于 $d$ ,因此可以将所有的 $k$ 按照 $d$ 分类。枚举所有的 $d$ ,对于每个 $d$ ,枚举 $n$ 的约数,则只需找出 $k$ 使得 $(\frac k d,\frac n d)=1$ 的个数即可,这个个数就是 $\varphi(\frac n d)$。
1 |
|