计算几何

前置知识点

1. $\pi=\arccos (-1)$

   $\cos(\pi)=-1,\arccos (\cos(\pi))=\arccos(-1)=\pi$

2. 余弦定理 $c^2=a^2+b^2-2ab\cos C$

3. 正弦定理 $\frac a {\sin A} =\frac b {\sin B}=\frac c {sinC}$

浮点数的比较

1
2
3
4
5
6
7
8
9
10
11

const double eps=1e-8;//精度
int sign(double x){
    if(fabs(x)<eps)return 0;//等于0
    if(x<0)return -1;//小于0
    return 1;//大于0
}
int cmp(double x,double y){
    if(fabs(x-y)<eps)return 0;//x=y
    if(x<y)return -1;//x<y
    return 1;//x>y
}

向量

设 $\vec {A}=(x_1,y_1),\vec{B}=(x_2,y_2)$

向量的加减法与数乘运算

$\vec{A}+\vec{B}=(x_1+x_2,y_1+y_2)$

$\vec{A}-\vec{B}=(x_1-x_2,y_1-y_2)$

$\lambda \vec A=(\lambda x_1,\lambda y_1)$

内积（点积）

$\vec A\cdot \vec B =|\vec A||\vec B|\cos \theta=x_1x_2+y_1y_2$

几何意义

向量 A 在向量 B 上的投影与 向量 B 的长度的乘积

代码实现

1
2
3

double dot(Point a,Point b){
    return a.x*b.x+a.y*b.y;
}

外积（叉积）

$\vec A\times \vec B=|\vec A||\vec B|\sin\theta=x_1y_2-x_2y_1$

几何意义

向量 A 与向量 B 张成的平行四边形的有向面积， B 在 A 的逆时针方向为正。

代码实现

1
2
3

double cross(Point a,Point b){
    return a.x*b.y-b.x*a.y;
}

常用函数

取模

$|\vec A|=\sqrt{x^2+y^2}$

1
2
3

double get_length(Point a){
    return sqrt(dot(a,a));
}

计算向量夹角

$\cos \theta =\frac{\vec A \cdot \vec B}{|\vec A||\vec B|}$

$\theta = \arccos(\cos \theta)$

1
2
3

double get_angle(Point a,Point b){
    return acos(dot(a,b)/get_length(a)/get_length(b));
}

计算两个向量构成的平行四边形有向面积

1
2
3

double area(Point a,Point b,Point c){
    return cross(b-a,c-a);
}

向量 A 顺时针旋转一定角度

设 $\vec A$ 与 x 轴夹角为 $\alpha$，要顺时针旋转 $\theta$，设旋转后的向量 $\vec{A’}=(x’,y’)$，则

$x’=|\vec A|\cos (\alpha-\theta)=\sqrt{x^2+y^2}(\cos \alpha \cos \theta+\sin \alpha \sin \theta)$

$y’=|\vec A| \sin(\alpha-\theta)=\sqrt{x^2+y^2}(\sin \alpha\cos \theta-\cos \alpha \sin \theta)$

由于 $\sin \alpha=\frac y {\sqrt{x^2+y^2}},\cos \alpha =\frac x{\sqrt{x^2+y^2}}$，所以

$x’= \sqrt{x^2+y^2}(\frac x{\sqrt{x^2+y^2}} \cos \theta+\frac y {\sqrt{x^2+y^2}} \sin \theta)=x\cos \theta+y\sin \theta$

$y’=\sqrt{x^2+y^2}(\frac y {\sqrt{x^2+y^2}}\cos \theta-\frac x{\sqrt{x^2+y^2}} \sin \theta)=y\cos\theta-x\sin\theta$

1
2
3

Point rotate(Point a,double angle){
    return Point(a.x*cos(angle)+a.y*sin(angle),-a.x*sin(angle)+a.y*cos(angle));
}

点与线

直线定理

1. 一般式：$ax+by+c=0$
2. 点向式：$P_0+t\vec v$ （$p_0$ 是一个点，$\vec v$ 是一个向量）
3. 斜截式：$y=kx+b$

常用操作

判断点在直线上

任取直线上的两个点构成的向量 $\vec A$ 和直线上一个点与需要判断的点构成的一个向量 $\vec B$，若 $\vec A \times \vec B=0$，则点在直线上

两直线相交

使用点向式表示两个直线，分别为 $P+t\vec v,Q+t\vec w$

首先判断两直线是否平行或重合 $\vec v \times \vec w=0 $

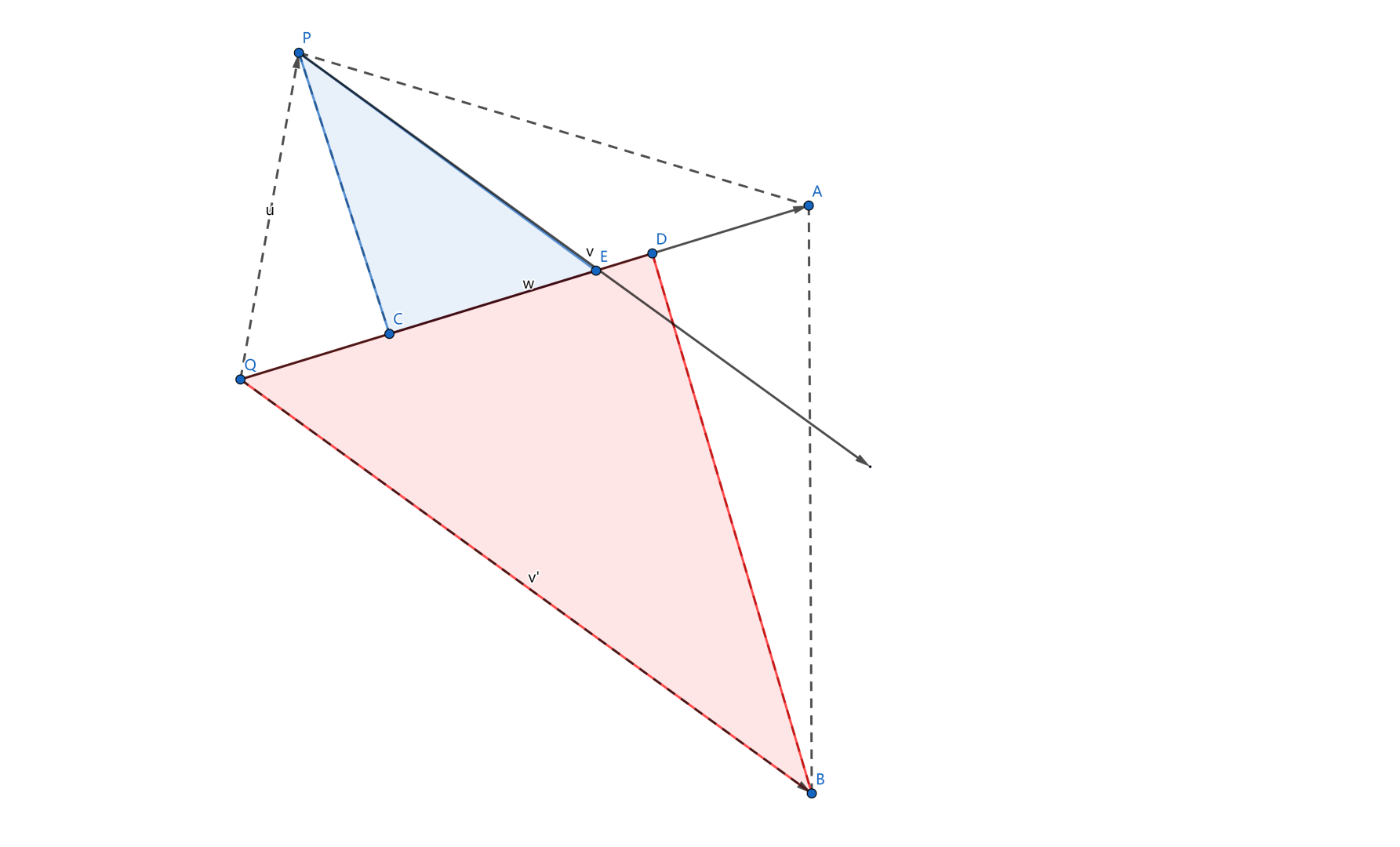
作出向量 $\vec {QP}$，即 $P-Q$，记为 $\vec u$， 连接 $PA$，则 $\vec u \times \vec w = 2S_{\triangle PQA}$，把向量 $\vec v$ 平移至点 $Q$，记为 $\vec {v’}$，连接 $AB$，则 $\vec v \times \vec w=\vec {v’} \times \vec w=2S_{\triangle AQB}$，所以 $t=\frac{\vec w \times \vec u}{\vec v \times \vec w}=\frac {S_{\triangle PQA}}{S_{\triangle AQB}}$

作 $PC \bot QA$ 于 $C$ ，$BD \bot QA$ 于 $D$ ，则$t=\frac {S_{\triangle PQA}}{S_{\triangle AQB}}=\frac {PC}{BD}$，易证 $\triangle PCE \sim \triangle BDQ$，相似比为 $\frac {PC}{BQ}=t$ ，所以 $\frac {PE} {BQ}=t,PE=t\vec v$，所以 交点 $E=P+t\vec v$。

1
2
3
4
5

Point get_line_intersection(Point p,Point v,Point q,Point w){
    Point u=p-q;
    double t=cross(w,u)/cross(v,w);
    return p+v*t;
}

点到直线的距离

设直线上两点 $A,B$，直线外一点 $P$，则距离 $d=\frac {2S_{\triangle PAB}}{AB}=\frac{|\vec{AP}\times \vec {AB}|}{|\vec {AB}|}$

1
2
3
4

double distance_to_line(Point p,Point a,Point b){
    Point v1=b-a,v2=p-a;
    return fabs(cross(v1,v2)/get_length(v1));
}

点到线段的距离

若 $A,B$ 重合，即点到点的距离

记点 $P$ 到线段 $AB$ 所在直线的垂线为点 $H$

若 $H$ 在 $A$ 的左侧，即 $\vec{AP} \cdot \vec{AB} <0$，则距离为 $PA$

若 $H$ 在 $B$ 的右侧，即 $\vec {BP} \cdot \vec{BA} <0, \vec {BP} \cdot \vec{AB} >0$，则距离为 $PB$

否则，距离为 $P$ 到 $AB$ 所在直线的距离。

1
2
3
4
5
6
7

double distance_to_segment(Point p,Point a,Point b){
    if(a==b)return get_length(p-a);
    Point v1=b-a,v2=p-a,v3=p-b;
    if(sign(dot(v1,v2))<0)return get_length(v2);
    if(sign(dot(v1,v3))>0)return get_length(v3);
    return distance_to_line(p,a,b);
}

点在直线上的投影

设直线上两点 $A,B$，直线外一点 $P$ ，记向量 $\vec{AP}$ 在向量 $\vec{AB}$ 上的投影为 $\vec{AC}=\frac {\vec{AB} \cdot \vec{AP}}{\vec{AB}^2} \vec{AB}$，则 $PC\bot AB$，所以 $C=A+\frac {\vec{AB} \cdot \vec{AP}}{\vec{AB}^2} \vec{AB}$ 即为所求

1
2
3
4

Point get_line_projection(Point p,Point a,Point b){
    Point v=b-a;
    return a+v*(dot(v,p-a)/dot(v,v));
}

点是否在线段上

设线段 $A,B$，点 $P$，则若 $\vec{AP}\cross \vec{BP}=0$，则 $P$ 在直线 $AB$ 上，若 $\vec {AP} \cdot \vec{BP}\le 0$，即两向量夹角为钝角，则 $P$ 在 $AB$ 之间。

1
2
3

bool on_segment(Point p,Point a,Point b){
    return sign(cross(p-a,p-b))==0&&sign(dot(p-a,p-b))<=0;
}

判断两线段是否相交

若 $(\vec {A_1A_2} \cross \vec{A_1B_1})(\vec {A_1A_2} \cross \vec{A_1B_2})\le 0$，则表示 $B_1,B_2$ 在线段 $A_1A_2$ 两侧，同理，若 $A_1,A_2$也在 $B_1B_2$ 两侧，则两线段相交

1
2
3
4
5

bool segment_intersection(Point a1,Point a2,Point b1,Point b2){
    double c1=cross(a2-a1,b1-a1),c2=cross(a2-a1,b2-a1);
    double c3=cross(b2-b1,a2-b1),c4=cross(b2-b1,a1-b1);
    return sign(c1)*sign(c2)<=0&&sign(c3)*sign(c4)<=0;
}

多边形

三角形

面积

1. 叉积 $S_{\triangle ABC}=\frac 1 2\vec{AB}\cross \vec{AC}$

2. 海伦公式

   设 $p=\frac{a+b+c} 2$，则 $S=\sqrt{p(p-a)(p-b)(p-c)}$

三角形四心

1. 外心，外接圆圆心

   三边中垂线交点，到三角形三个顶点的距离相等

2. 内心，内接圆圆心

   角平分线交点，到三边距离相等

3. 垂心

   三条垂线交点

4. 重心

   三条中线交点，到三角形三顶点距离的平方和最小的点，三角形内到三边距离之积最大的点

普通多边形

通常按逆时针存储所有点

定义

多边形

由在同一平面且不在同一直线上的多条线段首尾顺次连接且不相交所组成的图形叫多边形

简单多边形

除相邻边外其他边不相交的多边形叫简单多边形

凸多边形

过多边形的任意一边做一条直线，如果其他各个顶点都在这条直线的同侧，则把这个多边形叫做凸多边形

任意凸多边形外角和均为 $360\degree$

任意凸多边形的内角和为 $(n-2)180\degree$

常用函数

求多边形面积

从第一个顶点把多边形划分为 n-2 个三角形

1
2
3
4
5
6
7

double polygon_area(Point p[],int n){
    double s=0;
    for(int i=1;i+1<n;i++){
        s+=cross(p[i]-p[0],p[i+1]-p[i]);
    }
    return s/2;
}

判断点是否在多边形内

1. 射线法

   从该点任意做一条和所有边都不平行的射线，若与多边形的交点为奇数个，则点在多边形内，否则点在多边形外

2. 转角法

   计算点与一个顶点连线到下一个点的连线转过的角度，若角度之和为 $360\degree$，则点在多边形内，否则，点在多边形外

3. 判断点是否在凸多边形内

   只需判断点是否在所有边的左边，即点到每条边两段的向量的叉积为正即可。

皮克定理

皮克定理是指一个计算点阵中顶点在格点上的多边形面积公式，该公式可以表示为：

$S=a+\frac b 2 -1$

其中 $a$ 表示多边形内部的点数，$ b $ 表示多边形边界上的点数，$S$表示多边形的面积。

圆

圆的方程：$(x-a)^2+(y-b)^2=r^2$，直线的方程 $ax+by+c=0$，联立，解方程即可。