质数
定义:在大于一的整数中,如果只包含1和它本身两个约数,则被称为质数,也叫素数
质数的判定——试除法
若$n$小于2,则不是质数
从2开始,一直判定到$n-1$,若均无法整除,则为质数
1
2
3
4
5
6
7
| bool isprime(int x){
if(x<2)return 0;
for(int i=2;i<x;i++){
if(x%i==0)return 0;
}
return 1;
}
|
优化:可以发现,约数是成对出现的,所以只用循环到$\sqrt{n}$即可
1
2
3
4
5
6
7
8
| bool isprime(int x){
if(x<2)return 0;
int t=sqrt(x);
for(int i=2;i<=t;i++){
if(x%i==0)return 0;
}
return 1;
}
|
分解质因数——试除法
从小到大枚举$n$的约数,若整除,则为约数,此时求其次数
1
2
3
4
5
6
7
8
9
10
11
12
| void divide(int x){
for(int i=2;i<=x;i++){
if(x%i==0){
int s=0;
while(x%i==0){
x/=i;
s++;
}
cout << i << ' ' << s << endl;
}
}
}
|
考虑优化:
由于$n$中最多只包含一个大于$\sqrt{n}$的质因子,所以只需枚举到$n/i$,最后会剩余一个数,若这个数大于$n$,则此数为大于$\sqrt{n}$d的那个素因子,单独判断即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| void divide(int x){
for(int i=2;i<=x/i;i++){
if(x%i==0){
int s=0;
while(x%i==0){
x/=i;
s++;
}
cout << i << ' ' << s << endl;
}
}
if(x>1){
cout << x << ' ' << 1 << endl;
}
}
|
质数筛法
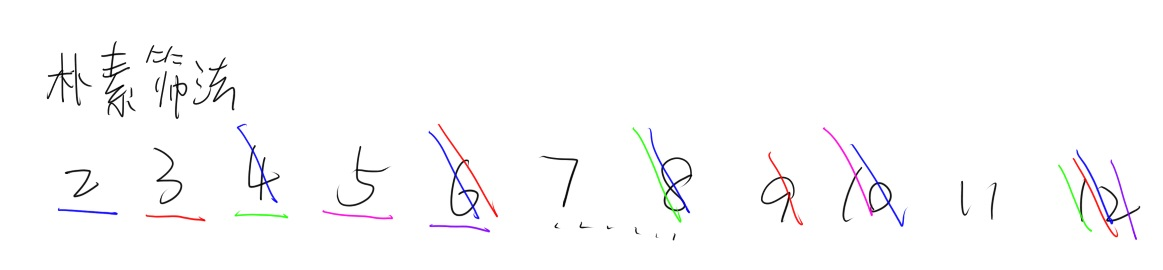
朴素筛法
每次循环每个数的倍数筛去

1
2
3
4
5
6
7
8
9
10
| bool st[N];
int prime[N],cnt;
void getprime(int n){
for(int i=2;i<=n;i++){
if(!st[i])prime[++cnt]=i;
for(int j=i*2;j<=n;j+=i){
st[j]=1;
}
}
}
|
复杂度$O(\log n)$
埃氏筛
每次筛时只筛素数的倍数
1
2
3
4
5
6
7
8
9
10
11
12
| bool st[N];
int prime[N],cnt;
void getprime(int n){
for(int i=2;i<=n;i++){
if(!st[i]){
prime[++cnt]=i;
for(int j=i*2;j<=n;j+=i){
st[j]=1;
}
}
}
}
|
复杂度$O(n\log \log n)$
线性筛
每个数只会被其最小质因子筛掉
循环,每次筛小于$n/i$的质数的$i$倍直到$i%prime_j=0$
每次筛数时:
- 若$i%prime_j=0$,则$prime_j$一定是$i$的最小质因子,$prime_j$也一定是$prime_j*i$的最小质因子
- 若$i%prime_j\not = 0$,,则$prime_j$一定小于$i$的所有质因子,$prime_j$也一定是$prime_j*i$的最小质因子
对于一个合数$x$,假设$prime_j$是$x$的最小质因子,当$i$枚举到$x/prime_j$时,一定会被筛掉
1
2
3
4
5
6
7
8
9
10
11
| bool st[N];
int prime[N],cnt;
void getprime(int n){
for(int i=2;i<=n;i++){
if(!st[i])prime[++cnt]=i;
for(int j=1;prime[j]<=n/i;j++){
st[prime[j]*i]=1;
if(i%prime[j]==0)break;
}
}
}
|
复杂度$O(n)$