Dancing Links X(DLX)

作用：优化搜索

题型：

1. 精确覆盖
2. 重复覆盖（配合IDA*）

前提：1的个数较少

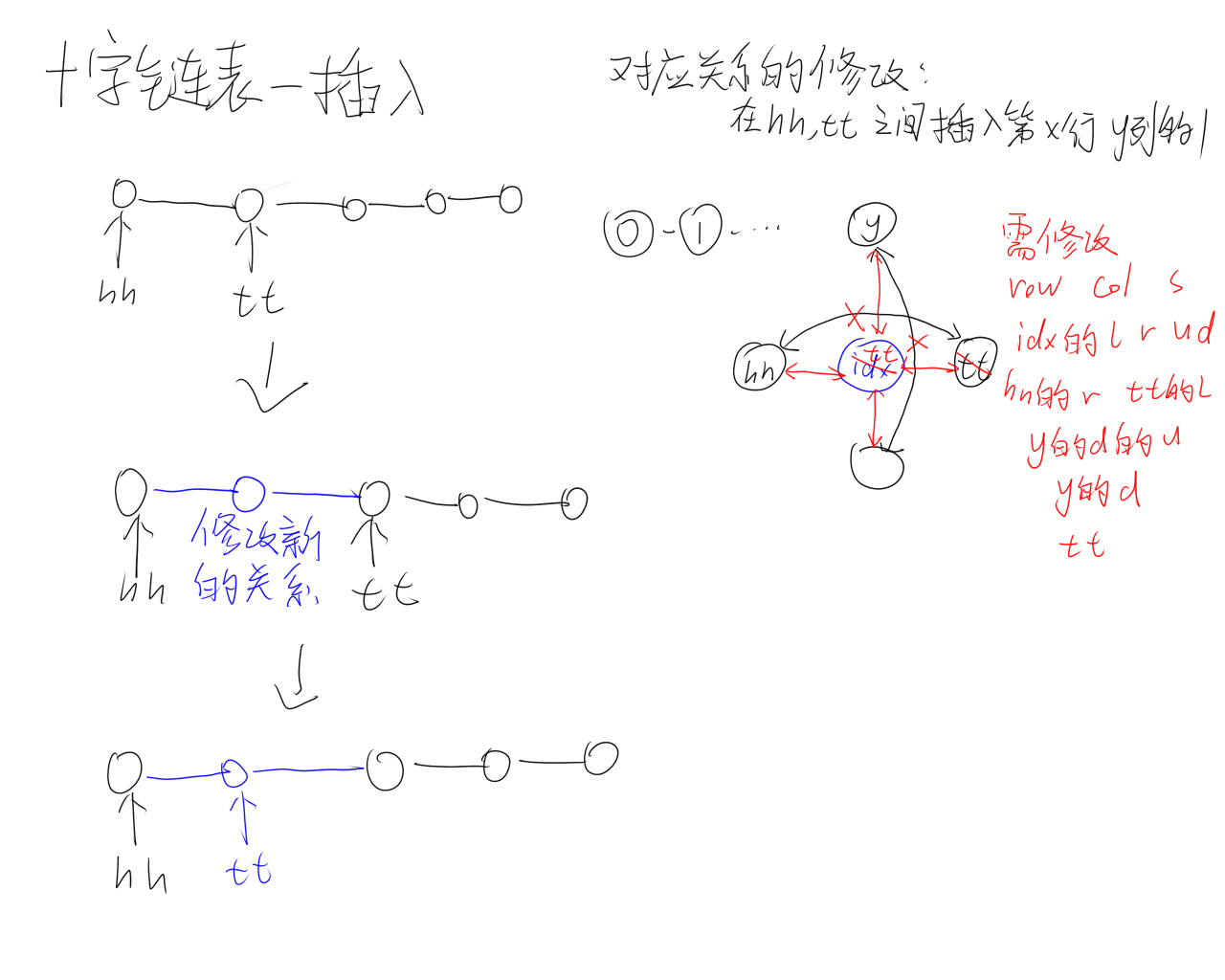
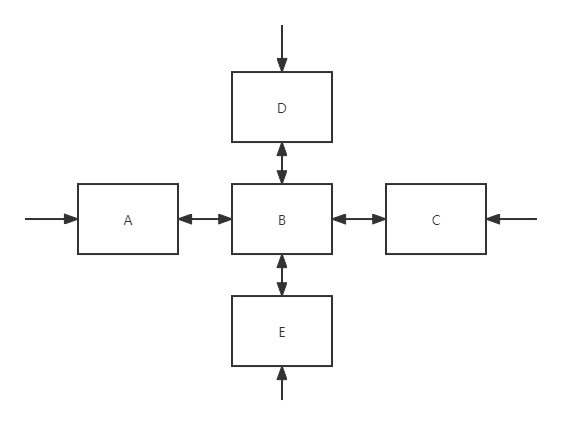
存储：十字链表:每个数指向上下左右第一个元素

1
2

int l[N],r[N],u[N],d[N],s[N],row[N],col[N],idx;
//  左指针，右指针，上指针，下指针，当前列1的个数，行号，列号

• 初始化：创建第零行(第$i$个的左指针为$i-1$，右指针为$i+1$，上下指针为自己

  1 2 3 4 5

  for(int i=0;i<=m;i++){ l[i]=i-1,r[i]=i+1,u[i]=d[i]=i; } l[0]=m,r[m]=0;//特判端点 idx=m+1;//一共用了m+1个点

• 每次加入一行

  维护当前行的第一个点$hh,tt$(初始均为$idx$)，每次插入一个点时插在$hh,tt$之间，修改对应关系，修改$hh$

  

  1 2 3 4 5 6

  int add(int &hh,int &tt,int x,int y){ row[idx]=x,col[idx]=y,s[y]++; u[idx]=y,d[idx]=d[y],u[d[y]]=idx,d[y]=idx; r[hh]=idx,l[tt]=idx,l[idx]=hh,r[idx]=tt; tt=idx++; }

  可以发现，建立完十字链表后可以用$d$从上到下查找，用$r$从左到右查找，用$l$从右到左查找

精确覆盖问题

给定一个 $ N \times M $ 的数字矩阵 $ A $，矩阵中的元素 $ A_{i,j} \in \lbrace 0,1 \rbrace $。

请问，你能否在矩阵中找到一个行的集合，使得这些行中，每一列都有且仅有一个数字 $ 1 $。

dfs：任意从未选择的行中选择一行

剪枝：

1. 选择1的个数最少的一列，枚举当前列有1的行

   1 2 3 4 5 6 7 8 9

   if(!r[0])return true;//若所有列都被删除，则已经找完所有列 int p=r[0]; for(int i=r[0];i;i=r[i]){ if(s[i]<=s[p])p=i; } //do something for(int i=d[p];i!=p;i=d[i]){ //do something }

2. 删除第$p$列

   可以发现，查找列时只会在第0列查找，所以只需删除第0列中的当前行，并在每个1所在的行删除（只需删除纵向即可跳过遍历）

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29

   void remove(int p){ r[l[p]]=r[p];l[r[p]]=l[p]; for(int i=d[p];i!=p;i=d[i]){ for(int j=r[i];j!=i;j=r[j]){ s[col[j]]--; u[d[j]]=u[j];d[u[j]]=d[j]; } } } void resume(int p){//逆方向恢复 r[l[p]]=p;l[r[p]]=p; for(int i=u[p];i!=p;i=u[i]){ for(int j=l[i];j!=i;j=l[j]){ s[col[j]]++; u[d[j]]=j;d[u[j]]=j; } } } bool dfs(){ ... remove(p); for(int i=d[p];i!=p;i=d[i]){ ... } resume(p); ... }

3. 删除选择的行中所有有1的列

   1 2 3 4 5 6 7 8 9 10

   bool dfs(){ ... for(int i=d[p];i!=p;i=d[i]){ ... for(int j=r[i];j!=i;j=r[j])remove(col[j]); ... for(int j=l[i];j!=i;j=l[j])resume(col[j]);//反向恢复 } ... }

总代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82

#include<bits/stdc++.h>
using namespace std;

const int N=5510;//5000+501

int n,m;
int l[N],r[N],u[N],d[N],s[N],row[N],col[N],idx;
int ans[N],top;

void init(){
    for(int i=0;i<=m;i++){
        l[i]=i-1,r[i]=i+1,u[i]=d[i]=i;
    }
    l[0]=m,r[m]=0;
    idx=m+1;
}

void add(int &hh,int &tt,int x,int y){
    row[idx]=x,col[idx]=y,s[y]++;
    u[idx]=y,d[idx]=d[y],l[idx]=hh,r[idx]=tt;
    u[d[y]]=idx,d[y]=idx,r[hh]=idx,l[tt]=idx;
    tt=idx++;
}

void remove(int p){
    r[l[p]]=r[p],l[r[p]]=l[p];
    for(int i=d[p];i!=p;i=d[i]){
        for(int j=r[i];j!=i;j=r[j]){
            s[col[j]]--;
            u[d[j]]=u[j],d[u[j]]=d[j];
        }
    }
}

void resume(int p){
    for(int i=u[p];i!=p;i=u[i]){
        for(int j=l[i];j!=i;j=l[j]){
            u[d[j]]=j,d[u[j]]=j;
            s[col[j]]++;
        }
    }
    r[l[p]]=p,l[r[p]]=p;
}

bool dfs(){
    if(!r[0])return true;
    int p=r[0];
    for(int i=r[0];i;i=r[i]){
        if(s[i]<s[p])p=i;
    }
    remove(p);
    for(int i=d[p];i!=p;i=d[i]){
        ans[++top]=row[i];
        for(int j=r[i];j!=i;j=r[j])remove(col[j]);
        if(dfs())return true;
        for(int j=l[i];j!=i;j=l[j])resume(col[j]);
        top--;
    }
    resume(p);
    return false;
}

int main(){
    cin >> n >> m;
    init();
    for(int i=1;i<=n;i++){
        int hh=idx,tt=idx;
        for(int j=1;j<=m;j++){
            int x;
            cin >> x;
            if(x)add(hh,tt,i,j);
        }
    }
    
    if(dfs()){
        for(int i=1;i<=top;i++)cout << ans[i] << ' ';
    }
    else{
        cout << "No Solution!";
    }
    return 0;
}

重复覆盖问题

给定一个 $ N \times M $ 的数字矩阵 $ A $，矩阵中的元素 $ A_{i,j} \in {0,1} $。

请你在矩阵中找到一个行的集合，使得这些行中，每一列都包含数字 $ 1 $，并且集合中包含的行数尽可能少。

dfs:

1. 选择一个空列(选择行数最少的列)

2. 枚举当前列是1的行

   枚举选当前行

   递归