KMP

作用：字符串匹配

例：给定一个$m$位字符串$s$，一个$n$位模式串$p$，求出$p$在$s$中所有出现的位置的起始下标

分析：

暴力算法：

1
2
3
4
5
6
7
8
9
10
11

char s[N],p[N];

for(int i=1;i<=m;i++){
    bool flag=true;
    for(int j=1;j<=n;j++){
        if(s[i+j-1]!=p[i]){
            flag=false;
            break;
        }
    }
}

考虑优化：

使用$ne[j]$记录$p$中$[1,j]$的前缀和后缀的最大相同长度，即$p$中$p[1,ne[j]]=p[j-ne[j]+1,j]$

$ne[j]$用于求若匹配失败则最少往后移动多少可以成功匹配。

用$j$表示模式串$p$已经有几位匹配成功，若$p[j]{=}\mathllap{/,}s[i+1]$，则表示当前位不匹配，此时把$p$向后移动$ne[j]$位即可保证$p[1\thicksim j-1]$再次匹配。

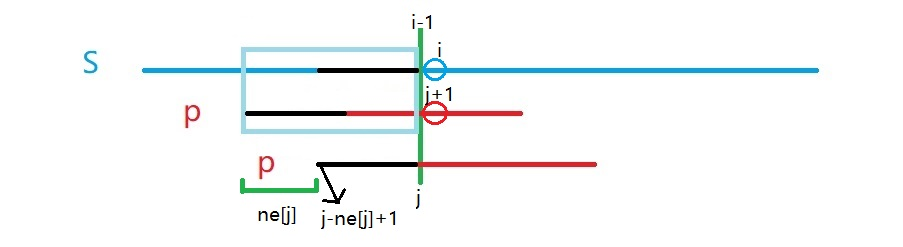
如上图，若在绿线之前均匹配，绿线之后不匹配，则最少把$p$向后移动$ne[j]$位至第二条线，此时三条黑线均相等。

由此，可以想到KMP的匹配：

• 若$j$没有退回起点且当前的$s[i]{=}\mathllap{/,}p[j+1]$，则把模式串向后移$ne[j]$位，此时的$j=ne[j]$，重复直至$s[i]=p[j+1]$
• 此时因为$s[i]=p[j+1]$，所以$p$中匹配的个数由$j$变成$j+1$，所以$j++$
• 若$j=n$，即模式串$p$完全匹配，则输出答案继续下一轮匹配($j=ne[j]$)

1
2
3
4
5
6
7
8

for(int i=1,j=0;i<=m;i++){
    while(j&&s[i]!=p[j+1])j=ne[j];
    if(s[i]==p[j+1])j++;
    if(j==n){
        cout << i-n+1 << ' ';
        j=ne[j];
    }
}

$ne$数组求法：例：$p=$”$abcab$”

$ne[1]$：前缀=$\phi$，后缀=$\phi$，$ne[1]=0$

$ne[2]$：前缀=${a}$，后缀=${b}$，$ne[2]=0$

$ne[3]$：前缀=${a,ab}$，后缀=${c,bc}$，$ne[3]=0$

$ne[4]$：前缀=${a,ab,abc}$，后缀=${a,ca,bca}$，$ne[4]=1$

$ne[5]$：前缀=${a,ab,abc,abca}$，后缀=${b,ab,cab,bcab}$，$ne[5]=2$

具体方法：类似KMP的匹配

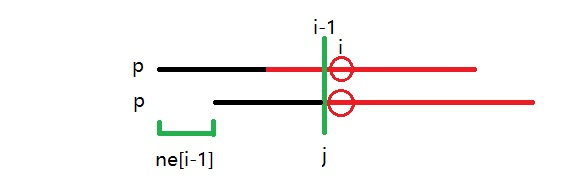
当$p[1\thicksim j]=p[j-ne[i-1]+1,j]$，且$p[i]{=}\mathllap{/,}p[j+1]$时，模式串$p$一直向后移（$j=ne[j]$）直至$p[i]=p[j+1]$，此时表示$[1,i]$的前后缀的相同最大长度为$j+1$，即$ne[i]=j+1$

步骤：

• 若$j$没有退回起点且当前的$s[i]{=}\mathllap{/,}p[j+1]$，则把模式串向后移$ne[j]$位，此时的$j=ne[j]$，重复直至$s[i]=p[j+1]$
• 此时因为$s[i]=p[j+1]$，所以$p$中匹配的个数由$j$变成$j+1$，所以$j++$
• 则$ne[i]=j$

1
2
3
4
5

for(int i=2,j=0;i<=n;i++){
    while(j&&p[i]!=p[j+1])j=ne[j];
    if(p[i]==p[j+1])j++;
    ne[i]=j;
}

总体代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

#include<bits/stdc++.h>
using namespace std;

const int N=1e4+5,M=1e5+5;

int n,m;
char s[M],p[N];
int ne[N];

int main(){
    cin >> n >> p+1 >> m >> s+1;
    //求next
    for(int i=2,j=0;i<=n;i++){
        while(j&&p[i]!=p[j+1])j=ne[j];
        if(p[i]==p[j+1])j++;
        ne[i]=j;
    }
    
    //kmp匹配
    for(int i=1,j=0;i<=m;i++){
        while(j&&s[i]!=p[j+1])j=ne[j];
        if(s[i]==p[j+1])j++;
        if(j==n){
            cout << i-n+1 << ' ';
            j=ne[j];
        }
    }
    return 0;
}