dp 技巧总结

P1020 [NOIP1999 提高组] 导弹拦截

以最长不下降子序列为例，时间复杂度为 $O(n \log n)$ 的一种算法：

记录每个长度的最长不下降子序列的结尾的最小值，可以发现有单调性，因此对于每个数二分查找可以接在哪一段后，更新即可。

1
2
3
4
5
6
7
8
9
10

for(int i=1;i<=n;i++){
    int l=0,r=len;
    while(l<r){
        int mid=l+r+1>>1;
        if(d[mid]>=a[i])l=mid;//如求上升/下降/不上升/公共，修改二分条件
        else r=mid-1;
    }
    len=max(len,l+1);
    d[l+1]=a[i];
}

Dilworth 定理

把序列划分成不下降子序列最少个数等于最长下降子序列长度

即有限偏序集中，最小链划分的个数等于最长反链长度

P1280 尼克的任务

如果一个状态受后面某些状态的影响，但不受前面状态的影响，可以逆序dp

P1439 【模板】最长公共子序列

朴素算法：d[i][j] 表示 A 中前 i 个元素，B 中前 j 个元素构成的最长公共子序列，易得出 a[i]==b[j] 时 d[i][j]=max(d[i][j],d[i-1][j-1]+1)

优化：由于A,B都是 1到n的排列，可以把A中的元素重新编号，变为 1,2,…,n，这样只需要在新的 B 中找到最长上升子序列即可。

P4301 绝世好题

出现位运算考虑是否可以按位dp优化时间复杂度

令dp[i]表示数列到目前为止最后一项第i位为1的最大子序列长度，每读入一个数时就转移。一个数可以被它所有的二进制位的dp值转移，然后把它转移到它的所有二进制位的dp值上。

P2516 [HAOI2010] 最长公共子序列

空间不够用滚动数组

背包问题

背包九讲

P1941 [NOIP2014 提高组] 飞扬的小鸟

首先，原始的转移方程：
$$
f[i][j]=min(f[i-1][j+y[i]],f[i-1][j-x[i]]+1,f[i-1][j-2 \times x[i]]+2,\cdots)
$$
但是这样的时间复杂度为 $O(nmk)$，会超时

观察转移方程：

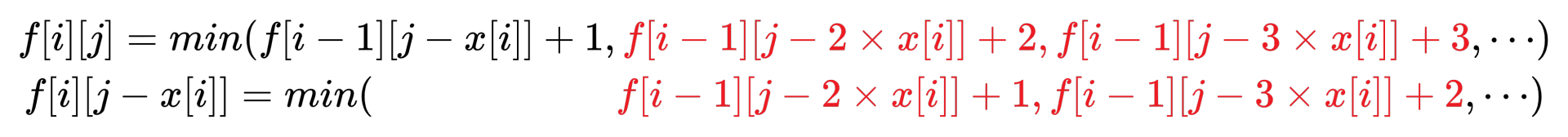
可以发现，红色部分十分相似，记右半部分为 $g[i][j]$，不难得到转移方程：
$$
g[i][j]=min(f[i-1][j-x[i]]+1,g[i][j-x[i]]+1)\
f[i][j]=min(f[i-1][j+y[i]],g[i][j])
$$
因此时间复杂度优化为 $O(nm)$

可以发现转移方程类似完全背包。