数论定理

欧几里得算法

已知两个数 $a,b$，记它们的最大公约数为 $\gcd(a,b)$ ，则有：

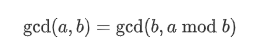
递归求解，当 $b=0$ 时 $\gcd(a,0)=a$。

时间复杂度 $O(\log a)$

1
2
3
4
5
6

int gcd(int a,int b){
    if(!b){
        return a;
    }
    return gcd(b,a%b);
}

扩展欧几里得算法

用于求形如 $ax+by=\gcd(a,b)$

过程：

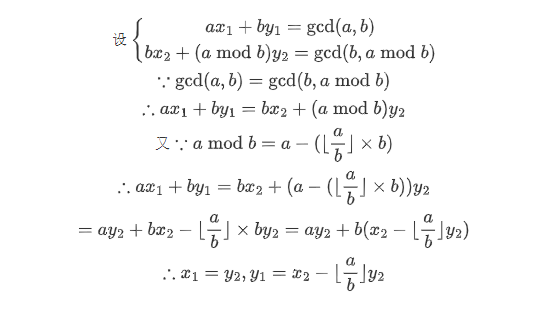
递归求解，当 $b=0$ 时，显然有一组解 $x=1,y=0$。

时间复杂度 $O(\log a)$

1
2
3
4
5
6
7
8
9

int exgcd(int a,int b,int &x,int &y){
    if(!b){
        x=1,y=0;
        return a;
    }
    int d=exgcd(b,a%b,y,x);
    y=y-a/b*x;
    return d;
}

欧拉函数

$\varphi(n)$ 表示小于等于 $n$ 的与 $n$ 互质的数的个数。

当 $n$ 为质数时，显然有 $\varphi(n)=n-1$。

性质：

• 欧拉函数是积性函数
• $n=\sum_{d|n} \varphi(d)$
• $\varphi(p^k)=p^k-p^{k-1}$，$p$ 是质数
• $n=\prod_{i=1}^{s} p_i^{k_i}$，则$\varphi(n)=n\times \prod_{i=1}^s \frac{p_i-1}{p_i}$
• $\varphi(mn)\varphi(\gcd(m,n))=\varphi(m)\varphi(n)\gcd(m,n)$

求单个欧拉函数值：使用第 4 条性质

求多个欧拉函数值：使用线性筛法（积性函数）

欧拉定理

若 $\gcd(a,m)=1$，则 $a^{\varphi(m)} \equiv 1 (\bmod m)$

扩展欧拉定理

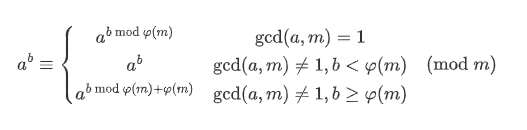
费马小定理

若 $p$ 是素数，$\gcd(a,p)=1$，则 $a^{p-1} \equiv 1 ( \bmod p)$

对于任意整数 $a$， 有 $a^p \equiv a (\bmod p)$

中国剩余定理

求解如下形式的一元线性同余方程组（其中 $n_1,n_2,\cdots ,n_k$ 两两互质）:

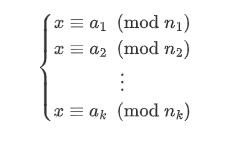
过程：

1. 计算 $n=\prod_{i=1}^k n_i$

2. 对于第 $i$ 个方程：

   计算 $m_i=\frac n {n_i}$

   计算 $m_i$ 在模 $n_i$ 意义下的逆元 $m_i^{-1}$

   计算 $c_i= m_i m_{i-1}$

3. 方程组在模 $n$ 意义下的唯一解为：$x=\sum_{i-1}^ka_ic_i\ \ (\bmod n)$

扩展：模数不互质的情况

两个方程

设方程为 $x \equiv a_1 (\bmod m_1)$ 、 $x \equiv a_2 (\bmod m_2)$

转化为 $x=m_1p+a_1=m_2q+a_2$，则有 $m_1p-m_2q=a_2-a_1$

用扩展欧几里得算法求出一组解 $(p,q)$

则两方程合并的解为 $x \equiv b (\bmod M)$，其中 $b=m_1p+a_1$，$M=\text{lcm}(m_1,m_2)$

多个方程

按两个方程的方法两两合并即可。

威尔逊定理

对于素数 $p$ 有 $(p-1)! \equiv -1 (\bmod p)$

卢卡斯定理

对于素数 $p$，有

1
2
3
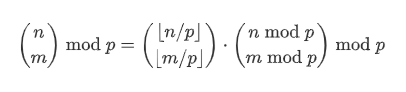
4

long long Lucas(long long n,long long m,long long p) {
    if(m==0)return 1;
    return (C(n%p,m%p,p)*Lucas(n/p,m/p,p))%p;
}