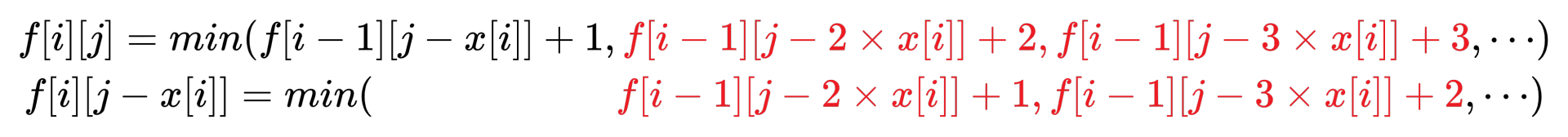Trick 总结

一般题的时间限制是 $1$ 秒或 $2$ 秒。
在这种情况下，C++代码中的操作次数控制在 $10^7 \sim 10^8$ 为最佳。

下面给出在不同数据范围下，代码的时间复杂度和算法该如何选择：

$n \le 30$, 指数级别, dfs+剪枝，状态压缩dp
$n \le 100$ => $O(n^3)$，floyd，dp，高斯消元
$n \le 1000$ => $O(n^2)$，$O(n^2 \log n)$，dp，二分，朴素版Dijkstra、朴素版Prim、Bellman-Ford
$n \le 10000$ => $O(n \sqrt n)$，块状链表、分块、莫队
$n \le 100000$ => $O(n \log n)$ => 各种sort，线段树、树状数组、set/map、heap、拓扑排序、dijkstra+heap、prim+heap、Kruskal、spfa、求凸包、求半平面交、二分、CDQ分治、整体二分、后缀数组、树链剖分、动态树
$n \le 1000000$ => $O(n)$, 以及常数较小的 $O(n \log n)$ 算法 => 单调队列、 hash、双指针扫描、BFS、并查集，kmp、AC自动机，常数比较小的 $O(n \log n)$ 的做法：sort、树状数组、heap、dijkstra、spfa
$n \le 10000000$ => $O(n)$，双指针扫描、kmp、AC自动机、线性筛素数
$n \le 10^9$ => $O(\sqrt n)$，判断质数
$n \le 10^{18}$ => $O(\log n)$，最大公约数，快速幂，数位DP
$n \le 10^{1000}$ => $O(\log^2n)$，高精度加减乘除
$n \le 10^{100000}$ => $O(\log k \times \log \log k)$，$k$ 表示位数，高精度加减、FFT/NTT

降维技巧

  • 求多个区间的值时可以前缀和优化 $O(n^2) \to O(n)$

    优化前：

    1
    2
    3
    4
    5
    for(int i=1;i<=q;i++){
        for(int j=l[i];j<=r[i];j++){
            sum+=f(a[i]);
        }
    }

    优化后：

    1
    2
    3
    4
    5
    6
    for(int i=1;i<=n;i++){
        s[i]=s[i-1]+f(a[i]);
    }
    for(int i=1;i<=q;i++){
        sum+=s[r[i]]-s[l[i]-1];
    }

  • 求高维前缀和时用分解法，即进行维数次一维前缀和，以三维为例：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            for (int k = 1; k <= n; k++)
                a[i][j][k] += a[i][j][k - 1];
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            for (int k = 1; k <= n; k++)
                a[i][j][k] += a[i][j - 1][k];
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            for (int k = 1; k <= n; k++)
                a[i][j][k] += a[i - 1][j][k];

  • 可以使用前缀和判断存在性，即令符合条件的点权值为1，否则为0，进行前缀和，判断一个区间是否存在符合条件的点就是判断这段区间的和是否不为0。

动态规划

  • 当数组太大导致空间不够时，可以使用滚动数组。

  • 以最长不下降子序列为例，时间复杂度为 $O(n\log⁡ n)$ 的一种算法：

    记录每个长度的最长不下降子序列的结尾的最小值，可以发现有单调性，因此对于每个数二分查找可以接在哪一段后，更新即可。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    for(int i=1;i<=n;i++){
        int l=0,r=len;
        while(l<r){
            int mid=l+r+1>>1;
            if(d[mid]>=a[i])l=mid;//如求上升/下降/不上升/公共，修改二分条件
            else r=mid-1;
        }
        len=max(len,l+1);
        d[l+1]=a[i];
    }

  • Dilworth 定理

    把序列划分成不下降子序列最少个数等于最长下降子序列长度。

    即有限偏序集中，最小链划分的个数等于最长反链长度。

  • 注意 dp 的后效性。如果一个状态受后面某些状态的影响，但不受前面状态的影响，可以逆序dp。

  • 当求 B 序列中一段 A 的子序列时，可以把 A 中元素编号为 1,2,… ，并修改 B 中元素的编号，则 B 中一段单调上升的子序列就是 A 的一个子序列。

    例题：P1439 【模板】最长公共子序列

    朴素算法：d[i][j] 表示 A 中前 i 个元素，B 中前 j 个元素构成的最长公共子序列，易得出 a[i]==b[j] 时 d[i][j]=max(d[i][j],d[i-1][j-1]+1)

    优化：由于A,B都是 1到n的排列，可以把A中的元素重新编号，变为 1,2,…,n，这样只需要在新的 B 中找到最长上升子序列即可。

  • 出现位运算考虑是否可以按位dp优化时间复杂度。

    例题：P4301 绝世好题

    令 $dp_i$ 表示数列到目前为止最后一项第 $i$ 位为 $1$ 的最大子序列长度，每读入一个数时就转移。一个数可以被它所有的二进制位的 dp 值转移，然后把它转移到它的所有二进制位的 dp 值上。

  • 背包九讲

  • 若 dp 的转移方程类似背包的转移，可以使用相同方式转化（主要是完全背包）。

    例题：P1941 [NOIP2014 提高组] 飞扬的小鸟

    首先，原始的转移方程：

    $f[i][j]=min(f[i−1][j+y[i]],f[i−1][j−x[i]]+1,f[i−1][j−2×x[i]]+2,⋯)$

    但是这样的时间复杂度为 $O(nmk)$，会超时

    观察转移方程：

    img

    可以发现，红色部分十分相似，记右半部分为 $g[i][j]$，不难得到转移方程：

    $g[i][j]=min(f[i−1][j−x[i]]+1,g[i][j−x[i]]+1)$

    $f[i][j]=min(f[i−1][j+y[i]],g[i][j])$

    因此时间复杂度优化为 $O(nm)$

    可以发现转移方程类似完全背包。

  • 当 $n \le 18$ 考虑状压 dp， 一维很小（如 $\le 100$）而另一维很大（如 $\le 10^9$）时考虑矩阵快速幂。

  • 当 dp 有特殊限制时，可以先 dfs 处理限制，再进行 dp

图论

  • 树上路径修改 $\to$ 树上差分

    • 点差分：b[s]++,b[t]++,b[fa[lca(s,t)]]--,b[lca(s,t)]--
    • 边差分：b[s]++,b[t]++,b[lca(s,t)]-=2

    求和时用 dfs ，从下向上加：

    1
    2
    3
    4
    for(auto x:to[u]){
        dfs(x);
        b[u]+=b[x];
    }

  • 当要求两条路径的并集的信息时，可以枚举交点。

  • 正难则反。如考虑删除最少等价于增加最大。

  • 连通性问题可以使用并查集。

  • 并查集很难删除，可以反向进行所有操作，把删除改为增加。

  • Floyd 最外层循环的意义：

    1
    2
    3
    4
    5
    6
    7
    for(int k=1;k<=n;k++){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
            }
        }
    }

    当枚举到 $k$ 时，$d_{i,j}$ 表示只经过 $1\sim k$ 的 $i$ 到 $j$ 的最短路径。

数据结构

  • 如果需要用线段树查询一段区间内的连续子区间的信息（即合并子节点信息时会跨越两段区间），可以使用三个参数 $mx,mxl,mxr$， 表示当前点的最大，包含左端点的最大和包含右端点的最大，这样转移时：
    $$
    mx[u]=\max{mx[son_l],mx[son_r],mxr[son_l]+mxl[son_r]}\
    mxl[u]=\max{mxl[son_l],sum_l+mxl[son_r]}\
    mxl[u]=\max{mxr[son_r],sum_r+mxr[son_l]}\
    $$
    例题：P4513 小白逛公园

  • 如果线段树需要进行取模、开方等，可以暴力修改并加上优化。

    优化：若取模，则当当前区间的最大值小于 $p$ 时直接返回。

    若开方，则当当前区间的最大值小于等于 $1$ 时直接返回。

数学

  • 见数论部分
许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。

快来参与讨论吧~